【题目】已知在△ABC中, a、b、c分别为角A、B、C的对边,且![]()
(1)若![]() ,试判断△ABC的形状;
,试判断△ABC的形状;
(2)若a=![]() ,b+c=3,求b和c的值.
,b+c=3,求b和c的值.
参考答案:
【答案】(1)△ABC是等边三角形(2)![]() 或
或![]()
【解析】试题分析:第一问主要是应用三角函数公式化简出三内角大小关系从而确定三角形形状;第二问借助于余弦定理找到边角间的关系式,从而解出边长
试题解析:(1)∵cos(B+C)=-cosA,
![]() 由2[1-cos(B+C)]-(2cos2A-1)=
由2[1-cos(B+C)]-(2cos2A-1)=![]() 得
得
∴4cos2A-4cosA+1=0, 4分
∴(2cosA-1)2=0,即cosA=![]() .
.
![]() ∴A=60°
∴A=60°
∵![]() ∴
∴![]()
∴![]() ,故△ABC是等边三角形
,故△ABC是等边三角形
(2)∵a2=b2+c2-2bccosA=b2+c2-bc=(b+c)2-3bc,
∵a=![]() ,b+c=3,∴3=9-3bc,∴bc=2,
,b+c=3,∴3=9-3bc,∴bc=2,
由![]() 解之得
解之得![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2=4,直线l:y=x,则圆C上任取一点A到直线l的距离小于1的概率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn , 若an+1+(﹣1)nan=n,则S40= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知当
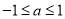 时,不等式
时,不等式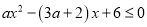 恒成立,求实数
恒成立,求实数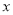 的取值范围
的取值范围(2)解关于
 的不等式
的不等式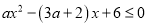 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设
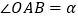 .(注:底面直径和高相等的圆柱叫做等边圆柱.)
.(注:底面直径和高相等的圆柱叫做等边圆柱.)(1)用
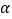 表示圆柱的高;
表示圆柱的高;(2)实践表明,当球心
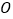 和圆柱底面圆周上的点
和圆柱底面圆周上的点 的距离达到最大时,景观的观赏效
的距离达到最大时,景观的观赏效果最佳,求此时
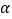 的值.
的值.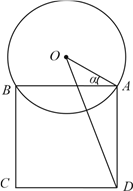
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数y=f(x)图象上不同两点A(x1 , y1),B(x2 , y2)处的切线的斜率分别是kA , kB , 规定φ(A,B)=
 (|AB|为线段AB的长度)叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: ①函数y=x3图象上两点A与B的横坐标分别为1和﹣1,则φ(A,B)=0;
(|AB|为线段AB的长度)叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: ①函数y=x3图象上两点A与B的横坐标分别为1和﹣1,则φ(A,B)=0;
②存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
③设点A,B是抛物线y=x2+1上不同的两点,则φ(A,B)≤2;
④设曲线y=ex(e是自然对数的底数)上不同两点A(x1 , y1),B(x2 , y2),则φ(A,B)<1.
其中真命题的序号为 . (将所有真命题的序号都填上) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 将
将 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数 的图象.
的图象.(1)求函数
 的解析式;
的解析式;(2)若方程
 在
在 上有且仅有一个实根,求
上有且仅有一个实根,求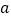 的取值范围;
的取值范围;(3)若函数
 与
与 的图象关于直线
的图象关于直线 对称,设
对称,设 ,已知
,已知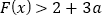 对任意的
对任意的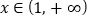 恒成立,求
恒成立,求 的取值范围.
的取值范围.
相关试题

