【题目】已知函数![]() 有两个不同的零点.
有两个不同的零点.
(1)求![]() 的取值范围;
的取值范围;
(2)记两个零点分别为![]() ,且
,且![]() ,已知
,已知![]() ,若不等式
,若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)方程![]() 在
在![]() 有两个不同跟等价于函数
有两个不同跟等价于函数![]() 与函数
与函数![]() 的图像在
的图像在![]() 上有两个不同交点,对
上有两个不同交点,对![]() 进行求导,通过单调性画出
进行求导,通过单调性画出![]() 的草图,由
的草图,由![]() 与
与![]() 有两个交点进而得出
有两个交点进而得出![]() 的取值范围; (Ⅱ)分离参数得:
的取值范围; (Ⅱ)分离参数得: ![]() ,从而可得
,从而可得![]() 恒成立;再令
恒成立;再令![]() ,从而可得不等式
,从而可得不等式![]() 在
在![]() 上恒成立,再令
上恒成立,再令![]() ,从而利用导数化恒成立问题为最值问题即可.
,从而利用导数化恒成立问题为最值问题即可.
试题解析:(I)依题意,函数![]() 的定义域为
的定义域为![]() ,
,
所以方程![]() 在
在![]() 有两个不同跟等价于函数
有两个不同跟等价于函数![]() 与函数
与函数![]() 的图像在
的图像在![]() 上有两个不同交点.
上有两个不同交点.
又![]() ,即当
,即当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
从而![]() .
.
又![]() 有且只有一个零点是1,且在
有且只有一个零点是1,且在![]() 时,
时, ![]() ,在
,在![]() 时,
时, ![]() ,
,
所以![]() 的草图如下:
的草图如下:
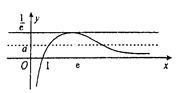
可见,要想函数![]() 与函数
与函数![]() 在图像
在图像![]() 上有两个不同交点,只需
上有两个不同交点,只需![]() .
.
(Ⅱ)由(I)可知![]() 分别为方程
分别为方程![]() 的两个根,即
的两个根,即![]() ,
, ![]() ,
,
所以原式等价于![]() .
.
因为![]() ,
, ![]() ,所以原式等价于
,所以原式等价于![]() .
.
又由![]() ,
, ![]() 作差得,
作差得, ![]() ,即
,即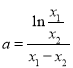 .
.
所以原式等价于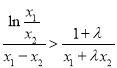 .
.
因为![]() ,原式恒成立,即
,原式恒成立,即![]() 恒成立.
恒成立.
令![]() ,则不等式
,则不等式![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,则
,则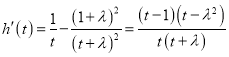 ,
,
当![]() 时,可见
时,可见![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]() 在
在![]() 恒成立,符合题意;
恒成立,符合题意;
当![]() 时,可见当
时,可见当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 时单调递增,在
时单调递增,在![]() 时单调递减.
时单调递减.
又![]() ,所以
,所以![]() 在
在![]() 上不能恒小于0,不符合题意,舍去.
上不能恒小于0,不符合题意,舍去.
综上所述,若不等式![]() 恒成立,只须
恒成立,只须![]() ,又
,又![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC的斜边BC在平面α内,则△ABC的两条直角边在平面α内的正射影与斜边组成的图形只能是( )
A.一条线段
B.一个锐角三角形或一条线段
C.一个钝角三角形或一条线段
D.一条线段或一个钝角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】设
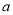 为实数,函数
为实数,函数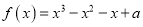 .
.(1)求
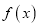 的极值;
的极值;(2)当
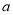 在什么范围内取值时,曲线
在什么范围内取值时,曲线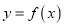 与
与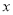 轴仅有一个交点?
轴仅有一个交点? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的方格纸由若干个边长为1的小正方形并在一起组成,方格纸中有两个定点A,B,点C为小正方形的顶点,且
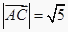
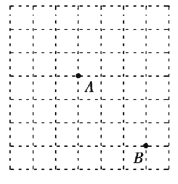
(1)画出所有的向量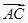 ;
;
(2)求| |的最大值与最小值.
|的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.y=x
B.y=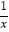
C.y=﹣x3
D.y=( )x
)x -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=loga(2﹣ax)是[0,1]上的减函数,则a的取值范围为 ( )
A. (0,1) B. (1,2) C. (0,2) D. (2,+∞)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣2x,g(x)=ax+2(a>0),且对任意的x1∈[﹣1,2],都存在x2∈[﹣1,2],使f(x2)=g(x1),则实数a的取值范围是( )
A.[3,+∞)
B.(0,3]
C.[ ,3]
,3]
D.(0, ]
]
相关试题

