【题目】为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取各10件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图:
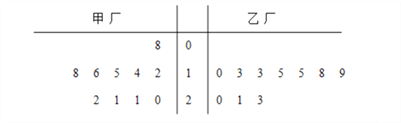
规定:当产品中的此种元素含量不小于16毫克时,该产品为优等品.
(1)从乙厂抽出的上述10件样品中,随机抽取3件,求抽到的3件样品中优等品数![]() 的分布列及其数学期望
的分布列及其数学期望![]() ;
;
(2)从甲厂的10件样品中有放回地逐个随机抽取3件,也从乙厂的10件样品中有放回地逐个随机抽取3件,求抽到的优等品数甲厂恰比乙厂多2件的概率.
参考答案:
【答案】(1)![]() ,分布列见解析(2)
,分布列见解析(2)![]()
【解析】试题分析:(1)![]() 的所有可能取值为
的所有可能取值为![]() ,由古典概型分别求概率,得到
,由古典概型分别求概率,得到![]() 的分布列,再求期望即可;(2)抽取的优等品数甲厂比乙厂多两件包括两个基本事件:
的分布列,再求期望即可;(2)抽取的优等品数甲厂比乙厂多两件包括两个基本事件:![]() “抽取的优等品数甲厂
“抽取的优等品数甲厂![]() 件,乙厂
件,乙厂![]() 件”,
件”,![]() “抽取的优等品数甲厂
“抽取的优等品数甲厂![]() 件,乙厂
件,乙厂![]() 件”,分别计算出它们的概率,再利用概率的加法公式得到抽取的优等品数甲厂恰比乙厂多
件”,分别计算出它们的概率,再利用概率的加法公式得到抽取的优等品数甲厂恰比乙厂多![]() 件的概率即可。
件的概率即可。
(1)由题意知,![]() 的值为0,1,2,3,
的值为0,1,2,3,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.
(2)甲厂抽取的样本中优等品有6件,优等品率为![]() ,
,
乙厂抽取的样本中有5件,优等品率为![]() ,
,
抽取的优等品数甲厂恰比乙厂多2件包括2个事件,
即![]() “抽取的优等品数甲厂2件,乙厂0件”,
“抽取的优等品数甲厂2件,乙厂0件”, ![]() “抽取的优等品数甲厂3件,乙厂1件”,
“抽取的优等品数甲厂3件,乙厂1件”,
![]() ,
,
![]() ,
,
∴抽到的优等品数甲厂恰比乙厂多2件的概率:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,
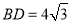 ,AB=2CD=8.
,AB=2CD=8.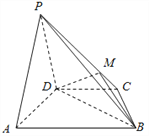
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
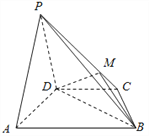
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,
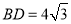 ,AB=2CD=8.
,AB=2CD=8.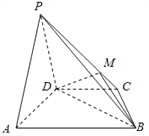
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
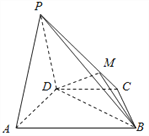
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
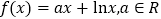 .
.(1)求函数
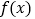 的极值;
的极值;(2)对于曲线上的不同两点
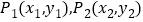 ,如果存在曲线上的点
,如果存在曲线上的点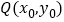 ,且
,且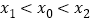 使得曲线在点
使得曲线在点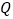 处的切线
处的切线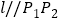 ,则称
,则称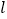 为弦
为弦 的伴随直线,特别地,当
的伴随直线,特别地,当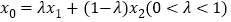 时,又称
时,又称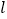 为
为 的
的 —伴随直线.
—伴随直线.①求证:曲线
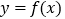 的任意一条弦均有伴随直线,并且伴随直线是唯一的;
的任意一条弦均有伴随直线,并且伴随直线是唯一的;②是否存在曲线
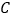 ,使得曲线
,使得曲线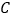 的任意一条弦均有
的任意一条弦均有 —伴随直线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.
—伴随直线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形
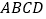 中,已知
中,已知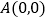 ,
,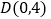 ,点
,点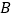 在
在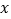 轴上,
轴上,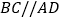 ,且对角线
,且对角线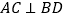 .
.(1)求点
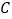 的轨迹
的轨迹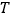 的方程;
的方程;(2)若点
 是直线
是直线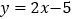 上任意一点,过点
上任意一点,过点 作点
作点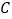 的轨迹
的轨迹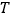 的两切线
的两切线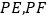 ,
,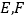 为切点,直线
为切点,直线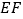 是否恒过一定点?若是,请求出这个定点的坐标;若不是,请说明理由.
是否恒过一定点?若是,请求出这个定点的坐标;若不是,请说明理由.
相关试题

