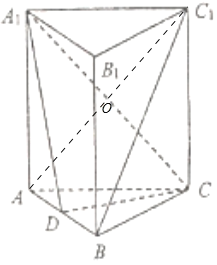
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)求证:![]() .
.
参考答案:
【答案】(1)见详解;(2)见详解.
【解析】
(1)连接AC1,设AC1∩A1C=O,连接OD,可求O为AC1的中点,D是棱AB的中点,利用中位线的性质可证OD∥BC1,根据线面平行的判断定理即可证明BC1∥平面A1CD.
(2)由(1)可证平行四边形ACC1A1是菱形,由其性质可得AC1⊥A1C,利用线面垂直的性质可证AB⊥AA1,根据AB⊥AC,利用线面垂直的判定定理可证AB⊥平面ACC1A1,利用线面垂直的性质可证AB⊥A1C,又AC1⊥A1C,根据线面垂直的判定定理可证A1C⊥平面ABC1,利用线面垂直的性质即可证明BC1⊥A1C.
(1)连接AC1,设AC1∩A1C=O,连接OD,在直三棱柱ABC﹣A1B1C1中,侧面ACC1A1是平行四边形,
所以:O为AC1的中点,又因为:D是棱AB的中点,所以:OD∥BC1,
又因为:BC1平面A1CD,OD平面A1CD,所以:BC1∥平面A1CD.
(2)由(1)可知:侧面ACC1A1是平行四边形,因为:AC=AA1,所以:平行四边形ACC1A1是菱形,
所以:AC1⊥A1C,在直三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,因为:AB平面ABC,所以:AB⊥AA1,
又因为:AB⊥AC,AC∩AA1=A,AC平面ACC1A1,AA1平面ACC1A1,
所以:AB⊥平面ACC1A1,因为:A1C平面ACC1A1,所以:AB⊥A1C,
又因为:AC1⊥A1C,AB∩AC1=A,AB平面ABC1,AC1平面ABC1,所以:A1C⊥平面ABC1,
因为:BC1平面ABC1,所以:BC1⊥A1C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3﹣x2=2.(12分)
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)如图,在平面直角坐标系xOy中,依次连接点P1(x1 , 1),P2(x2 , 2)…Pn+1(xn+1 , n+1)得到折线P1 P2…Pn+1 , 求由该折线与直线y=0,x=x1 , x=xn+1所围成的区域的面积Tn .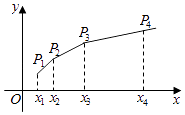
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}为等差数列,前n项和为Sn(n∈N+),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4﹣2a1 , S11=11b4 .
(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{a2nb2n﹣1}的前n项和(n∈N+). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
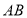 是半圆
是半圆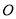 的直径,
的直径, 垂直于半圆
垂直于半圆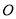 所在的平面,点
所在的平面,点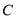 是圆周上不同于
是圆周上不同于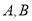 的任意一点,
的任意一点,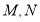 分别为
分别为 的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )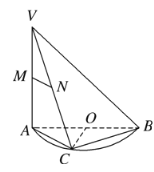
A.
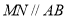 B.平面
B.平面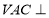 平面
平面
C.
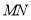 与
与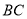 所成的角为45°D.
所成的角为45°D. 平面
平面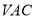
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列
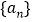 满足,
满足,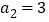 ,
,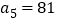 .
.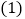 求数列
求数列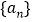 的通项公式;
的通项公式; 设
设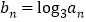 ,求
,求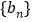 的前n项和为
的前n项和为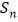 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:A、B、C三地位于同一水平面上,在C处进行该仪器的垂直弹射,观测点A、B两地相距100米,∠BAC=60°,在A地听到弹射声音的时间比在B地晚
 秒. A地测得该仪器弹至最高点H时的仰角为30°.
秒. A地测得该仪器弹至最高点H时的仰角为30°.(1)求A、C两地的距离;
(2)求该仪器的垂直弹射高度CH.(声音的传播速度为340米/秒)

-
科目: 来源: 题型:
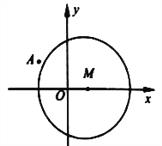
查看答案和解析>>【题目】如图,已知圆
 :
: 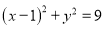 ,点
,点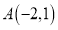 .
.
(1)求经过点
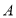 且与圆
且与圆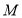 相切的直线
相切的直线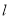 的方程;
的方程;(2)过点
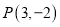 的直线与圆
的直线与圆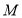 相交于
相交于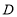 、
、 两点,
两点, 为线段
为线段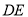 的中点,求线段
的中点,求线段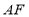 长度的取值范围.
长度的取值范围.
相关试题

