【题目】已知数列![]() 中,
中,![]() , 且
, 且![]() .
.
(1)求![]() 的值及数列
的值及数列![]() 的通项公式;
的通项公式;
(2)令![]() , 数列
, 数列![]() 的前
的前![]() 项和为
项和为![]() , 试比较
, 试比较![]() 与
与![]() 的大小;
的大小;
(3)令![]() , 数列
, 数列 的前
的前![]() 项和为
项和为![]() , 求证: 对任意
, 求证: 对任意![]() , 都有
, 都有![]() .
.
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)令![]() ,求得
,求得![]() ,同理令
,同理令![]() ,求得
,求得![]() .对
.对![]() 两边除以
两边除以![]() ,得到
,得到![]() ,利用累加法求得
,利用累加法求得![]() ,所以
,所以![]() ;(2)化简
;(2)化简![]() ,则
,则![]() ,.记函数
,.记函数![]() ,利用
,利用![]() 可得当
可得当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(3)化简
;(3)化简![]() ,故
,故 ,利用放缩法
,利用放缩法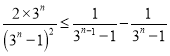 ,利用裂项求和法证得
,利用裂项求和法证得![]() .
.
试题解析:
(1)当![]() 时,
时,![]() , 当
, 当![]() 时,
时,![]() ,因为
,因为![]() ,所以
,所以![]() ,当
,当![]() 时,由累加法得
时,由累加法得![]() , 因为
, 因为![]() ,所以
,所以![]() 时,有
时,有![]() ,即
,即![]() ,又
,又![]() 时,
时,![]() ,故
,故![]() .
.
(2)![]() 时,
时,![]() ,则
,则![]() .
.
记函数![]() ,所以
,所以![]() ,
,
则![]() ,所以
,所以![]() .由于
.由于
![]() ,此时
,此时![]() ,
,![]() ,此时
,此时![]() ,
,
![]() ,此时
,此时![]() ,由于
,由于![]() ,故
,故![]() 时,
时,![]() ,此时
,此时![]() .综上所述,当
.综上所述,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(3)证明: 对于![]() ,有
,有 ,
,
当![]() 时,
时, .所以当
.所以当![]() 时,
时,
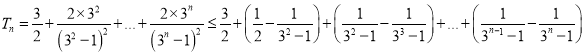
![]() .且
.且![]() .故对
.故对![]() 得证.
得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知棱长为l的正方体
 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且 ,设面
,设面 面MPQ=
面MPQ= ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )
A.
 面ABCD
面ABCDB.
 AC
ACC.面MEF与面MPQ不垂直
D.当x变化时,
 不是定直线
不是定直线 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某隧道设计为双向四车道,车道总宽为
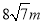 ,要求通行车辆限高
,要求通行车辆限高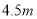 ,隧道全长为
,隧道全长为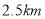 ,隧道的拱线可近似的看成半个椭圆形状.
,隧道的拱线可近似的看成半个椭圆形状.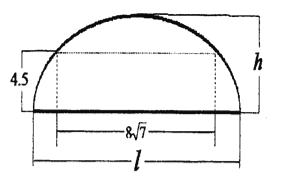
(1)若最大拱高
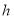 为
为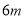 ,则隧道设计的拱宽
,则隧道设计的拱宽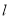 是多少?
是多少?(2)若最大拱高
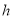 不小于
不小于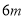 ,则应如何设计拱高
,则应如何设计拱高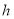 和拱宽
和拱宽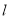 ,才能使隧道的土方工程量最小?
,才能使隧道的土方工程量最小?(注: 1.半个椭圆的面积公式为
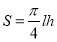 ;2.隧道的土方工程量=截面面积
;2.隧道的土方工程量=截面面积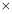 隧道长)
隧道长) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当x∈[1,4]时,求函数
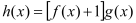 的值域;
的值域;(2)如果对任意的x∈[1,4],不等式
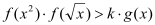 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】在长方体
 中,
中,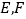 分别是
分别是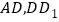 的中点,
的中点,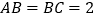 ,过
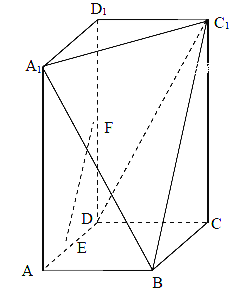
,过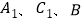 三点的的平面截去长方体的一个角后.得到如图所示的几何体
三点的的平面截去长方体的一个角后.得到如图所示的几何体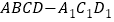 ,且这个几何体的体积为
,且这个几何体的体积为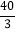 .
.
(1)求证:
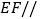 平面
平面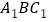 ;
;(2)求
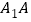 的长;
的长;(3)在线段
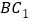 上是否存在点
上是否存在点 ,使直线
,使直线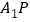 与
与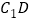 垂直,如果存在,求线段
垂直,如果存在,求线段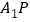 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列问题中符合调查问卷要求的是( )
A.你们单位有几个高个子?
B.您对我们厂生产的电视机满意吗?
C.您的体重是多少千克?
D.很多顾客都认为该产品的质量很好,您不这么认为吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①已知集合
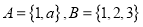 ,则“
,则“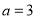 ”是“
”是“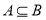 ”的充分不必要条件;
”的充分不必要条件;②“
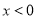 ”是“
”是“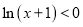 ”的必要不充分条件;
”的必要不充分条件;③“函数
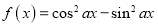 的最小正周期为
的最小正周期为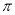 ”是“
”是“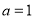 ”的充要条件;
”的充要条件;④“平面向量
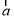 与
与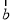 的夹角是钝角”的要条件是“
的夹角是钝角”的要条件是“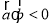 ”.
”.其中正确命题的序号是 .(把所有正确命题的序号都写上)
相关试题

