【题目】如图,某隧道设计为双向四车道,车道总宽为![]() ,要求通行车辆限高
,要求通行车辆限高![]() ,隧道全长为
,隧道全长为![]() ,隧道的拱线可近似的看成半个椭圆形状.
,隧道的拱线可近似的看成半个椭圆形状.
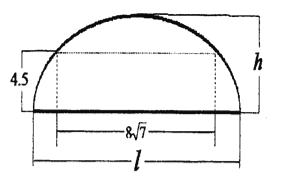
(1)若最大拱高![]() 为
为![]() ,则隧道设计的拱宽
,则隧道设计的拱宽![]() 是多少?
是多少?
(2)若最大拱高![]() 不小于
不小于![]() ,则应如何设计拱高
,则应如何设计拱高![]() 和拱宽
和拱宽![]() ,才能使隧道的土方工程量最小?
,才能使隧道的土方工程量最小?
(注: 1.半个椭圆的面积公式为![]() ;2.隧道的土方工程量=截面面积
;2.隧道的土方工程量=截面面积![]() 隧道长)
隧道长)
参考答案:
【答案】(1)32![]() ;(2)当拱高为
;(2)当拱高为![]() ,拱宽为
,拱宽为![]() 时,土方工程量最小.
时,土方工程量最小.
【解析】
试题分析:本题是椭圆的实际应用题,考查利用椭圆标准方程解应用题.(1)以车道中点为原点,建立直角坐标系,则![]() 在椭圆上,这时椭圆方程可设为
在椭圆上,这时椭圆方程可设为![]() ,由
,由![]() 及
及![]() 点坐标可求得椭圆中的
点坐标可求得椭圆中的![]() ,从而得结论;(2)隧道的土方工程量最小即半椭圆的面积最小,即椭圆的面积为
,从而得结论;(2)隧道的土方工程量最小即半椭圆的面积最小,即椭圆的面积为![]() 最小,利用标准方程及基本不等式可求得
最小,利用标准方程及基本不等式可求得![]() 的最小值.
的最小值.
试题解析:(1)以车道中点为原点,建立直角坐标系,则![]() ,
,
设椭圆的方程为![]() ,则
,则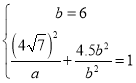 解之得:
解之得:![]() ,
,
此时![]() .
.
(2)由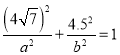 ,可知
,可知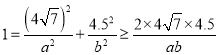 ,
,
故![]() ,所以
,所以![]() ,
,
当且仅当![]() 时取等号,
时取等号,
答:当拱高为![]() ,拱宽为
,拱宽为![]() 时,土方工程量最小.
时,土方工程量最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量
 (件)与单价
(件)与单价 (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(1)根据周销售量图写出
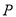 (件)与单价
(件)与单价 (元)之间的函数关系式;
(元)之间的函数关系式;(2)写出利润
 (元)与单价
(元)与单价 (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润. -
科目: 来源: 题型:
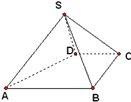
查看答案和解析>>【题目】如图,四棱锥
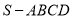 中,
中, 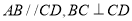 ,侧面
,侧面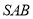 为等边三角形,
为等边三角形, 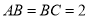 ,
, 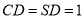 .
.
(Ⅰ)证明:
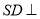 平面
平面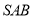 ;
;(Ⅱ)求
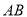 与平面
与平面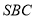 所成的角的大小.
所成的角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知棱长为l的正方体
 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且 ,设面
,设面 面MPQ=
面MPQ= ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )
A.
 面ABCD
面ABCDB.
 AC
ACC.面MEF与面MPQ不垂直
D.当x变化时,
 不是定直线
不是定直线 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当x∈[1,4]时,求函数
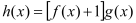 的值域;
的值域;(2)如果对任意的x∈[1,4],不等式
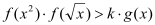 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
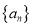 中,
中,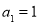 , 且
, 且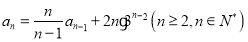 .
.(1)求
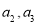 的值及数列
的值及数列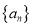 的通项公式;
的通项公式;(2)令
 , 数列
, 数列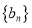 的前
的前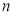 项和为
项和为 , 试比较
, 试比较 与
与 的大小;
的大小;(3)令
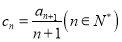 , 数列
, 数列 的前
的前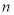 项和为
项和为 , 求证: 对任意
, 求证: 对任意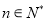 , 都有
, 都有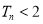 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在长方体
 中,
中,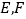 分别是
分别是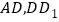 的中点,
的中点,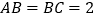 ,过
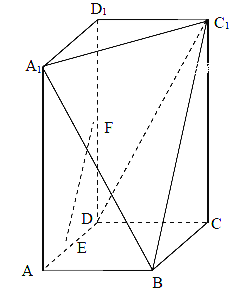
,过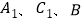 三点的的平面截去长方体的一个角后.得到如图所示的几何体
三点的的平面截去长方体的一个角后.得到如图所示的几何体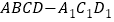 ,且这个几何体的体积为
,且这个几何体的体积为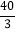 .
.
(1)求证:
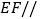 平面
平面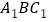 ;
;(2)求
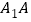 的长;
的长;(3)在线段
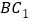 上是否存在点
上是否存在点 ,使直线
,使直线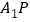 与
与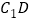 垂直,如果存在,求线段
垂直,如果存在,求线段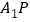 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
相关试题

