【题目】如图,已知椭圆![]() 经过不同的三点
经过不同的三点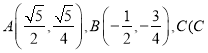 在第三象限),线段
在第三象限),线段![]() 的中点在直线
的中点在直线![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
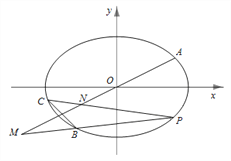
(Ⅱ)设点![]() 是椭圆
是椭圆![]() 上的动点(异于点
上的动点(异于点![]() 且直线
且直线![]() 分别交直线
分别交直线![]() 于
于![]() 两点,问
两点,问![]() 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)点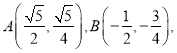 的坐标代入椭圆的方程就可求得方程,设点
的坐标代入椭圆的方程就可求得方程,设点![]() 的坐标,根据条件可得点
的坐标,根据条件可得点![]() 的坐标代入椭圆方程,BC中点坐标代入直线
的坐标代入椭圆方程,BC中点坐标代入直线![]() 的方程,两方程联立可求点
的方程,两方程联立可求点![]() 的坐标;(2)设
的坐标;(2)设![]() ,根据
,根据![]() 三点共线,用点P的坐标
三点共线,用点P的坐标![]() 表示
表示![]() ,同理用点P的坐标
,同理用点P的坐标![]() 表示
表示![]() 。再求
。再求![]() 为定值,所以
为定值,所以![]() 。
。
试题解析:(Ⅰ)由点![]() 在椭圆
在椭圆![]() 上,得
上,得 解得
解得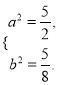 所以椭圆
所以椭圆![]() 的方程为
的方程为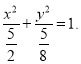 ………………………3分
………………………3分
由已知,求得直线![]() 的方程为
的方程为![]() 从而
从而![]() (1)
(1)
又点![]() 在椭圆
在椭圆![]() 上,故
上,故![]() (2)
(2)
由(1)(2)解得![]() (舍去)或
(舍去)或![]() 从而
从而![]()
所以点![]() 的坐标为
的坐标为![]() ………………………………………6分
………………………………………6分
(Ⅱ)设![]()
因![]() 三点共线,故
三点共线,故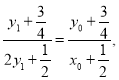 整理得
整理得![]()
因![]() 三点共线,故
三点共线,故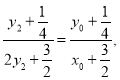 整理得
整理得![]() ……………10分
……………10分
因点![]() 在椭圆
在椭圆![]() 上,故
上,故![]() ,即
,即![]()
从而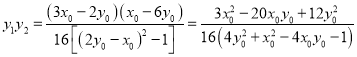
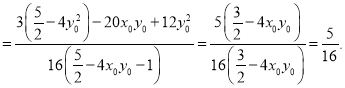
所以![]() 为定值. ………………………15分
为定值. ………………………15分
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如下表:
学生编号
1
2
3
4
5
6
语文成绩

60
70
74
90
94
110
历史成绩
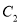
58
63
75
79
81
88
(1)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(2)用上表数据画出散点图易发现历史成绩
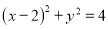 与语文成绩
与语文成绩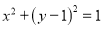 具有较强的线性相关关系,求
具有较强的线性相关关系,求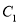 与
与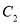 的线性回归方程(系数精确到0.1).
的线性回归方程(系数精确到0.1).参考公式:回归直线方程是
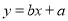 ,其中
,其中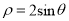 ,
, 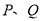
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下2×2的列联表:
喜欢该项运动
不喜欢该项运动
总计
男
40
20
60
女
20
30
50
总计
60
50
110
由公式
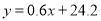 ,算得
,算得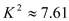
附表:
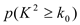
0.025
0.01
0.005
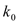
5.024
6.635
7.879
参照附表,以下结论正确是( )
A. 有
 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”B. 有
 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”C. 有
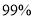 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”D. 有
 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关” -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
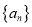 中,满足
中,满足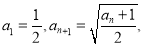 记
记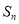 为
为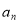 前n项和.
前n项和.(I)证明:
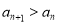 ;
;(Ⅱ)证明:

(Ⅲ)证明:
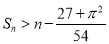 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lg
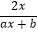 ,f(1)=0,且f(2)﹣f(
,f(1)=0,且f(2)﹣f(  )=lg2.
)=lg2.
(1)求f(x)的表达式;
(2)若x∈(0,+∞)时方程f(x)=lgt有解,求实数t的取值范围;
(3)若函数y=f(x)﹣lg(8x+m)的无零点,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在矩形
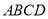 中,
中, 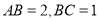 ,
, 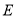 是
是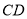 的中点,将三角形
的中点,将三角形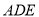 沿
沿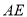 翻折到图②的位置,使得平面
翻折到图②的位置,使得平面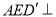 平面
平面 .
.(Ⅰ)在线段
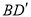 上确定点
上确定点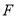 ,使得
,使得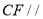 平面
平面 ,并证明;
,并证明;(Ⅱ)求
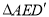 与
与 所在平面构成的锐二面角的正切值.
所在平面构成的锐二面角的正切值. 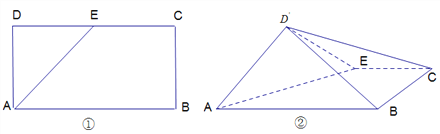
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蛋糕店每天做若干个生日蛋糕,每个制作成本为50元,当天以每个100元售出,若当天白天售不出,则当晚以30元/个价格作普通蛋糕低价售出,可以全部售完.
(1)若蛋糕店每天做20个生日蛋糕,求当天的利润
 (单位:元)关于当天生日蛋糕的需求量
(单位:元)关于当天生日蛋糕的需求量 (单位:个,
(单位:个,  )的函数关系;
)的函数关系;(2)蛋糕店记录了100天生日蛋糕的日需求量(单位:个)整理得下表:

(ⅰ)假设蛋糕店在这100天内每天制作20个生日蛋糕,求这100天的日利润(单位:元)的平均数;
(ⅱ)若蛋糕店一天制作20个生日蛋糕,以100天记录的各需求量的频率作为概率,求当天利润不少于900元的概率.
相关试题

