【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某测观点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时)
参考答案:
【答案】(1) 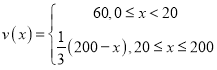 (2) 当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3 333辆/小时
(2) 当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3 333辆/小时
【解析】
试题分析:(1)设v(x)=ax+b.利用x的范围,列出方程组求解a,b,即可得到函数的解析式;(2)求出车流量f(x)=v(x)x的表达式,然后求解最大值即可
试题解析:(1)由题意:当0≤x≤20时,v(x)=60;
当20≤x≤200时,设v(x)=ax+b,
再由已知得![]() 解得
解得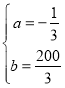 故函数v(x)的表达式为
故函数v(x)的表达式为
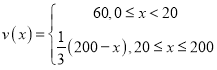
(2)依题意并由(1)可得
f(x)=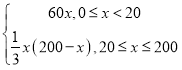
当0≤x≤20时,f(x)为增函数,故当x=20时,其最大值为60×20=1200;
当20≤x≤200时,f(x)=![]() x(200-x)≤
x(200-x)≤![]() [
[![]() ]2=
]2=![]() ,
,
当且仅当x=200-x,即x=100时,等号成立.
所以,当x=100时,f(x)在区间上取得最大值![]() .
.
综上,当x=100时,f(x)在区间上取得最大值![]() ≈3 333,
≈3 333,
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3 333辆/小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列结论中正确的是( )
A. 在复平面上,x轴叫做实轴,y轴叫做虚轴 B. 任何两个复数都不能比较大小
C. 如果实数a与纯虚数ai对应,那么实数集与纯虚数集是一一对应的 D. -1的平方根是i
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知函数
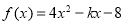 在
在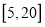 上具有单调性,求实数
上具有单调性,求实数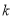 的取值范围.
的取值范围.(2)关于x的方程mx2+2(m+3)x+2m+14=0有两个不同的实根,且一个大于4,另一个小于4,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱
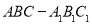 的底面是边长为2的正三角形,
的底面是边长为2的正三角形,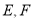 分别是
分别是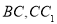 的中点。
的中点。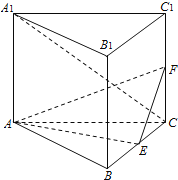
(1)证明:平面
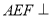 平面
平面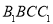 ;
;(2)若直线
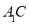 与平面
与平面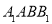 所成的角为
所成的角为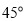 ,求三棱锥
,求三棱锥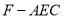 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列表示图书借阅的流程正确的是( )
A. 入库→阅览→借书→找书→出库→还书 B. 入库→找书→阅览→借书→出库→还书
C. 入库→阅览→借书→找书→还书→出库 D. 入库→找书→阅览→借书→还书→出库
-
科目: 来源: 题型:
查看答案和解析>>【题目】类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四面体的下列性质,你认为比较恰当的是 ( )
①各棱长相等,同一顶点上的任意两条棱的夹角都相等;
②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;
③各个面都是全等的正三角形,同一顶点上的任意两条棱的夹角都相等.
A. ① B. ③ C. ①② D. .①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两城相距100 km,在两地之间距A城x km处的D地建一核电站给A,B两城供电.为保证城市安全,核电站与城市距离不得少于10 km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数λ=0.25.若A城供电量为20亿度/月,B城为10亿度/月.
(1)求x的取值范围;
(2)把月供电总费用y表示成x的函数;
(3)核电站建在距A城多远,才能使供电费用最小?
相关试题

