【题目】如图,边长为4的正方形ABCD所在平面与正三角形PAD所在平面互相垂直,M,Q分别为PC,AD的中点. 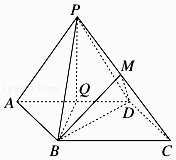
(1)求证:PA∥平面MBD;
(2)求二面角P﹣BD﹣A的余弦值.
参考答案:
【答案】
(1)证明:连接AC、BD交于点O,连接OM.
则AO=OC,又PM=MC,
∴PA∥OM.
∵PA平面BMD,OM平面BMD,
∴PA∥平面BMD

(2)证明:解:以A为原点,AB为x轴,AD为y轴,过A作平面ABCD的垂线为z轴,
建立空间直角坐标系,
则P(0,2,2 ![]() ),B(4,0,0),D(0,4,0),
),B(4,0,0),D(0,4,0),
![]() =(﹣4,2,2
=(﹣4,2,2 ![]() ),
), ![]() =(﹣4,4,0),
=(﹣4,4,0),
设平面BPD的法向量 ![]() =(x,y,z),
=(x,y,z),
则 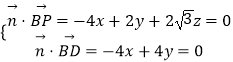 ,
,
取x=1,得 ![]() =(1,1,
=(1,1, ![]() ),
),
平面ABD的法向量 ![]() =(0,0,1),
=(0,0,1),
设二面角P﹣BD﹣A的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
∴二面角P﹣BD﹣A的余弦值为 ![]()
【解析】(1)连接AC、BD交于点O,连接OM,推导出PA∥OM,由此能证明PA∥平面BMD.(2)以A为原点,AB为x轴,AD为y轴,过A作平面ABCD的垂线为z轴,建立空间直角坐标系,利用向量法能求出二面角P﹣BD﹣A的余弦值.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x+sin|x|,x∈[﹣π,π]的大致图象是( )
A.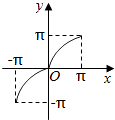
B.
C.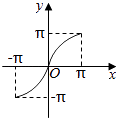
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平行四边形ABB1A1中,∠ABB1=60°,AB=4,AA1=2,C,C1分别为AB,A1B1的中点,现把平行四边形ABB1A1沿CC1折起如图2所示,连接B1C,B1A,B1A1 .
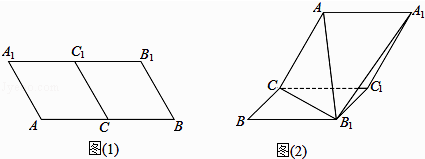
(1)求证:AB1⊥CC1;
(2)若AB1=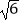 ,求二面角C﹣AB1﹣A1的余弦值.
,求二面角C﹣AB1﹣A1的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若偶函数f(x)在区间[﹣1,0]上是减函数,α,β是锐角三角形的两个内角,且α≠β,则下列不等式中正确的是( )
A.f(cosα)>f(cosβ)
B.f(sinα)<f(cosβ)
C.f(cosα)<f(sinβ)
D.f(sinα)>f(sinβ) -
科目: 来源: 题型:
查看答案和解析>>【题目】设
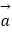 、
、 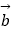 为平面向量,若存在不全为零的实数λ,μ使得λ
为平面向量,若存在不全为零的实数λ,μ使得λ 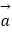 +μ
+μ 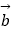 =0,则称
=0,则称 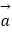 、
、 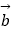 线性相关,下面的命题中,
线性相关,下面的命题中, 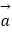 、
、 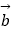 、
、 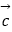 均为已知平面M上的向量. ①若
均为已知平面M上的向量. ①若 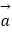 =2
=2 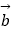 ,则
,则 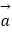 、
、 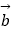 线性相关;
线性相关;
②若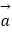 、
、 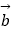 为非零向量,且
为非零向量,且 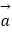 ⊥
⊥ 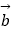 ,则
,则 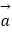 、
、 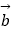 线性相关;
线性相关;
③若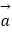 、
、 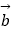 线性相关,
线性相关, 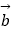 、
、 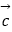 线性相关,则
线性相关,则 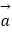 、
、 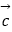 线性相关;
线性相关;
④向量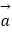 、
、 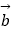 线性相关的充要条件是
线性相关的充要条件是 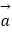 、
、 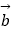 共线.
共线.
上述命题中正确的是(写出所有正确命题的编号) -
科目: 来源: 题型:
查看答案和解析>>【题目】设两个非零向量
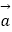 与
与  不共线.
不共线.
(1)若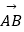 =
= 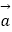 +
+  ,
, 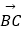 =2
=2 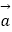 +8
+8  ,
,  =3(
=3( 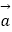 ﹣
﹣  ).求证:A,B,D三点共线;
).求证:A,B,D三点共线;
(2)试确定实数k,使k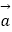 +
+  和
和 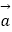 +k
+k  共线.
共线. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
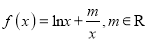
(Ⅰ)当
 (
( 为自然对数的底数)时,求
为自然对数的底数)时,求 的极小值;
的极小值;(Ⅱ)若函数
 存在唯一零点,求
存在唯一零点,求 的取值范围.
的取值范围.
相关试题

