【题目】函数y=x+sin|x|,x∈[﹣π,π]的大致图象是( )
A.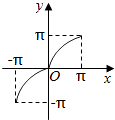
B.
C.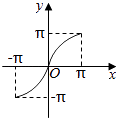
D.
参考答案:
【答案】A
【解析】解:由题意可知: ![]() ,
,
当0≤x≤π时,∵y=x+sinx,∴y′=1+cosx≥0,所以函数y=x+sinx在[0,π]上为增函数;
又由sinx≥0[0,π]上恒成立,故函数y=x+sinx[0,π]上在y=x的上方;
当﹣π≤x<0时,∵y=x﹣sinx,∴y′=1﹣cosx≥0,所以函数y=x+sinx在[0,π]上为增函数;
又由sinx≤0[﹣π,0]上恒成立,故函数y=x+sinx[﹣π,0]上在y=x的下方;
又函数y=x+sin|x|,x∈[﹣π,π],恒过(﹣π,﹣π)和(π,π)两点,所以A选项对应的图象符合.
故选A.
【考点精析】根据题目的已知条件,利用函数的图象的相关知识可以得到问题的答案,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:k2﹣8k﹣20≤0,命题q:方程
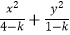 =1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
=1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
(Ⅱ)若命题“p∨q”为真,命题“p∧q”为假,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的前n项和为Sn , S3=﹣15,且a1+1,a2+1,a4+1成等比数列,公比不为1.
(1)求数列{an}的通项公式;
(2)设bn=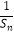 ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=sin(x﹣
 )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移
)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移  个单位,得到的图象对应的解析式是( )
个单位,得到的图象对应的解析式是( )
A.
B.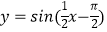
C.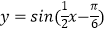
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平行四边形ABB1A1中,∠ABB1=60°,AB=4,AA1=2,C,C1分别为AB,A1B1的中点,现把平行四边形ABB1A1沿CC1折起如图2所示,连接B1C,B1A,B1A1 .
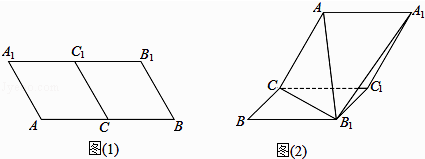
(1)求证:AB1⊥CC1;
(2)若AB1=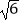 ,求二面角C﹣AB1﹣A1的余弦值.
,求二面角C﹣AB1﹣A1的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若偶函数f(x)在区间[﹣1,0]上是减函数,α,β是锐角三角形的两个内角,且α≠β,则下列不等式中正确的是( )
A.f(cosα)>f(cosβ)
B.f(sinα)<f(cosβ)
C.f(cosα)<f(sinβ)
D.f(sinα)>f(sinβ) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为4的正方形ABCD所在平面与正三角形PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
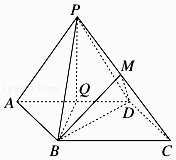
(1)求证:PA∥平面MBD;
(2)求二面角P﹣BD﹣A的余弦值.
相关试题

