【题目】已知双曲线方程为![]() .
.
(1)求以定点![]() 为中点的弦所在的直线方程;
为中点的弦所在的直线方程;
(2)以定点![]() 为中点的弦存在吗?若存在,求出其所在的直线方程;若不存在,请说明理由.
为中点的弦存在吗?若存在,求出其所在的直线方程;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)不存在,理由见解析
;(2)不存在,理由见解析
【解析】
(1)设以定点![]() 为中点的弦的端点坐标为
为中点的弦的端点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,运用中点坐标公式和直线的斜率公式,运用点差法可得所求直线的斜率,再由点斜式方程即可得到所求直线方程;
,运用中点坐标公式和直线的斜率公式,运用点差法可得所求直线的斜率,再由点斜式方程即可得到所求直线方程;
(2)假设定点![]() 为中点的弦存在,设以定点
为中点的弦存在,设以定点![]() 为中点的弦的端点坐标为
为中点的弦的端点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,运用中点坐标公式和直线的斜率公式,结合点差法,求得直线的斜率,由点斜式方程可得直线方程,代入双曲线的方程,检验判别式是否大于0,即可判断是否存在.
,运用中点坐标公式和直线的斜率公式,结合点差法,求得直线的斜率,由点斜式方程可得直线方程,代入双曲线的方程,检验判别式是否大于0,即可判断是否存在.
解:(1)设以定点![]() 为中点的弦的端点坐标为
为中点的弦的端点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,①
,①
由端点在双曲线上,可得![]() ,
,![]() ,
,
两式相减可得![]() ,
,
将①代入上式,
可得以定点![]() 为中点的弦所在的直线斜率为
为中点的弦所在的直线斜率为
![]() ,
,
则以定点![]() 为中点的弦所在的直线方程为
为中点的弦所在的直线方程为![]() ,
,
即为![]() ,
,
代入双曲线的方程可得![]() ,
,
由![]() ,可得所求直线存在,
,可得所求直线存在,
即有所求直线的方程为![]() ;
;
(2)假设定点![]() 为中点的弦存在,
为中点的弦存在,
设以定点![]() 为中点的弦的端点坐标为
为中点的弦的端点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,②
,②
由端点在双曲线上,可得![]() ,
,![]() ,
,
两式相减可得![]() ,
,
将②代入上式,
可得以定点![]() 为中点的弦所在的直线斜率为
为中点的弦所在的直线斜率为
![]() ,
,
则以定点![]() 为中点的弦所在的直线方程为
为中点的弦所在的直线方程为![]() ,
,
即为![]() ,
,
代入双曲线的方程可得![]() ,
,
由![]() ,可得所求直线不存在,
,可得所求直线不存在,
以定点![]() 为中点的弦不存在.
为中点的弦不存在.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断正确的是( )
A.
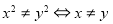 或
或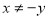
B.命题“若
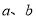 都是偶数,则
都是偶数,则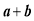 是偶数”的逆否命题是“若
是偶数”的逆否命题是“若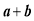 不是偶数,则
不是偶数,则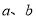 都不是偶数”
都不是偶数”C.若“
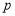 或
或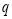 ”为假命题,则“非
”为假命题,则“非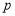 且非
且非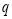 ”是真命题
”是真命题D.已知
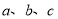 是实数,关于
是实数,关于 的不等式
的不等式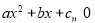 的解集是空集,必有
的解集是空集,必有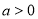 且
且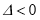
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)在y=x2的函数图象上.
(1)求数列{an}的通项公式;
(2)若bn=(-1)n+1anan+1,求数列{bn}的前100项和T100.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
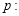 实数
实数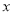 满足
满足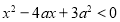 ,其中
,其中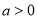 .
.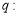 实数
实数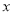 满足
满足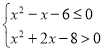 .
.(1)若
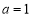 ,且
,且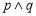 为真,求实数
为真,求实数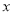 的取值范围;
的取值范围;(2)非
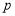 是非
是非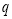 的充分不必要条件,求实数
的充分不必要条件,求实数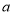 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥A-BCD中,AB=a,AC=AD=b,BC=CD=DB=c(a>0,b>0,c>0)该三棱锥的截面EFGH平行于AB、CD,分别交AD、AC、BC、BD于E、F、G、H.

(1)证明:AB⊥CD;
(2)求截面四边形EFGH面积的最大值,并说明面积取最大值时截面的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,直线l过点P(1,2).
(1)若直线l在x轴和y轴上的截距相等,求直线l的方程;
(2)求坐标原点O到直线l距离取最大值时的直线l的方程;
(3)设直线l与x轴正半轴、y轴正半轴分别相交于A,B两点,当|PA||PB|最小时,求直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
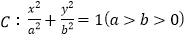 的左焦点为
的左焦点为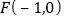 ,离心率
,离心率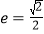 .
.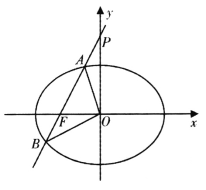
(I)求椭圆C的标准方程;
(II)已知直线
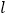 交椭圆C于A,B两点.
交椭圆C于A,B两点.①若直线
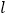 经过椭圆C的左焦点F,交y轴于点P,且满足
经过椭圆C的左焦点F,交y轴于点P,且满足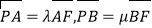 .求证:
.求证: 为定值;
为定值;②若
 ,求
,求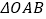 面积的取值范围.
面积的取值范围.
相关试题

