搜索
【题目】某几何体的主视图和左视图如图（1），它的俯视图的直观图是矩形O1A1B1C1如图（2），其中O1A1=6，O1C1=2，则该几何体的侧面积为（ ）
A.48
B.64
C.96
D.128
参考答案：
【答案】C
【解析】解：由已知中的三视图可得该几何体是一个四棱柱，
∵它的俯视图的直观图是矩形O1A1B1C1 ， O1A1=6，O1C1=2，
∴它的俯视图的直观图面积为12，
∴它的俯视图的面积为：24 
，
∴它的俯视图
的俯视图是边长为：6的菱形，
棱柱的高为4
故该几何体的侧面积为：4×6×4=96，
故选：C．
【考点精析】解答此题的关键在于理解由三视图求面积、体积的相关知识，掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有甲、乙两个班进行数学考试，按照大于等于120分为优秀，120分以下为非优秀统计成绩后，得到如下
列联表：（单位：人）. 
已知在全部105人中随机抽取1人成绩是优秀的概率为
.（1）请完成上面的
列联表，并根据表中数据判断，是否有
的把握认为“成绩与班级有关系”？（2）若甲班优秀学生中有男生6名，女生4名，现从中随机选派3名学生参加全市数学竞赛，记参加竞赛的男生人数为
，求
的分布列与期望.附：
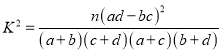
0.15
0.10
0.050
0.010
2.072
2.706
3.841
6.635
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=xm﹣
，且f（3）= 
．
（1）求函数f（x）的解析式，并判断函数f（x）的奇偶性．
（2）证明函数f（x）在（0，+∞）上的单调性． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=（
）x ， 其反函数为y=g（x）．
（1）若g（mx2+2x+1）的定义域为R，求实数m的取值范围；
（2）当x∈[﹣1，1]时，求函数y=[f（x）]2﹣2af（x）+3的最小值h（a）；
（3）是否存在实数m＞n＞3，使得函数y=h（x）的定义域为[n，m]，值域为[n2 ， m2]，若存在，求出m、n的值；若不存在，则说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】直线l交椭圆4x2+5y2=80于M、N两点，椭圆的上顶点为B点，若△BMN的重心恰好落在椭圆的右焦点上，则直线l的方程是（ ）
A.5x+6y﹣28=0
B.5x﹣6y﹣28=0
C.6x+5y﹣28=0
D.6x﹣5y﹣28=0 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=（ex+1）（ax+2a﹣2），若存在x∈（0，+∞），使得不等式f（x）﹣2＜0成立，则实数a的取值范围是（ ）
A.（0，1）
B.（0，
）
C.（﹣∞，1）
D.（﹣∞，
） -
科目： 来源： 题型：
查看答案和解析>>【题目】某企业生产A，B两种产品，根据市场调查与市场预测，A产品的利润与投资成正比，其关系如图（1）；B产品的利润与投资的算术平方根成正比，其关系如图（2）（注：所示图中的横坐标表示投资金额，单位为万元）
（1）分别求出A，B两种产品的利润表示为投资的函数关系式；
（2）该企业已筹集到10万元资金，并全部投入A，B两种产品的生产，问：怎样分配这10万元资金，才能使企业获得最大利润，最大利润是多少？
相关试题
