【题目】设![]() 是
是![]() 在点
在点![]() 处的切线.
处的切线.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)设![]() ,其中
,其中![]() .若
.若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)
;(Ⅱ)见解析;(Ⅲ) ![]() .
.
【解析】试题分析:(Ⅰ)由导数值得切线斜率,进而得切线方程,即可求函数f(x)的解析式;
(Ⅱ)令![]() ,求导证得
,求导证得![]() ;
;
(Ⅲ)![]() ,① 当
,① 当![]() 时,由(Ⅰ)得
时,由(Ⅰ)得 ![]() ,可得
,可得![]() ,进而得
,进而得![]() 在区间
在区间![]() 上单调递增,
上单调递增, ![]() 恒成立,② 当
恒成立,② 当![]() 时,可得
时,可得![]() 在区间
在区间![]() 上单调递增,存在
上单调递增,存在![]() ,使得
,使得![]() ,
, ![]() ,此时
,此时![]() 不会恒成立,进而得的取值范围.
不会恒成立,进而得的取值范围.
试题解析:
(Ⅰ)设![]() ,则
,则![]() ,所以
,所以![]() .
.
所以![]() .
.
(Ⅱ)令![]() .
.
![]() 满足
满足![]() ,且
,且![]() .
.
当![]() 时,
时, ![]() ,故
,故![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,故
,故![]() 单调递增.
单调递增.
所以, ![]()
![]() ).
).
所以![]() .
.
(Ⅱ)![]() 的定义域是
的定义域是![]() ,且
,且![]() .
.
① 当![]() 时,由(Ⅰ)得
时,由(Ⅰ)得 ![]() ,
,
所以 ![]() .
.
所以 ![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以 ![]() 恒成立,符合题意.
恒成立,符合题意.
② 当![]() 时,由
时,由![]() ,
,
且![]() 的导数
的导数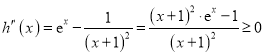 ,
,
所以 ![]() 在区间
在区间![]() 上单调递增.
上单调递增.
因为 ![]() ,
, ![]() ,
,
于是存在![]() ,使得
,使得![]() .
.
所以 ![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以 ![]() ,此时
,此时![]() 不会恒成立,不符合题意.
不会恒成立,不符合题意.
综上, ![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知95个数a1,a2,a3,…,a95,
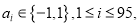 则a1a2+a1a3+…+a94a95的最小正值是______________.
则a1a2+a1a3+…+a94a95的最小正值是______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
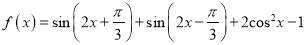 ,
, 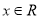 .
.(1)求函数
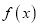 的最小正周期;
的最小正周期;(2)求函数
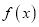 在区间
在区间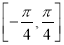 上的最大值和最小值.
上的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
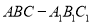 中,侧棱
中,侧棱 底面
底面 ,
,  为棱
为棱 中点.
中点. 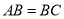 ,
,  ,
,  .
.
(I)求证:
 平面
平面 .
.(II)求证:
 平面
平面 .
.(III)在棱
 的上是否存在点
的上是否存在点 ,使得平面
,使得平面 平面
平面 ?如果存在,求此时
?如果存在,求此时 的值;如果不存在,说明理由.
的值;如果不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于数集
 ,其中
,其中 ,
,  ,定义向量集
,定义向量集 .若对于任意
.若对于任意 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .例如
.例如 具有性质
具有性质 .
.(
 )若
)若 ,且
,且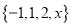 具有性质
具有性质 ,求
,求 的值.
的值.(
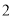 )若
)若 具有性质
具有性质 ,求证:
,求证:  ,且当
,且当 时,
时,  .
.(
 )若
)若 具有性质
具有性质 ,且
,且 ,
,  (
( 为常数),求有穷数列
为常数),求有穷数列 ,
,  ,
,  ,
,  的通项公式.
的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
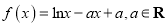 .
.(1)求函数
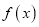 的单调区间;
的单调区间;(2)当
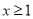 时,函数
时,函数 的图象恒不在
的图象恒不在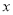 轴的上方,求实数
轴的上方,求实数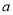 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
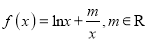
(Ⅰ)当
 (
( 为自然对数的底数)时,求
为自然对数的底数)时,求 的极小值;
的极小值;(Ⅱ)若函数
 存在唯一零点,求
存在唯一零点,求 的取值范围.
的取值范围.
相关试题

