【题目】已知函数是定义在上的偶函数,且当时,.
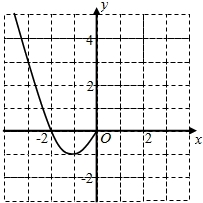
(1)现已画出函数在轴左侧的图象,如图所示,请补出完整函数的图象,并根据图象写出函数的增区间;
(2)写出函数的解析式和值域.
参考答案:
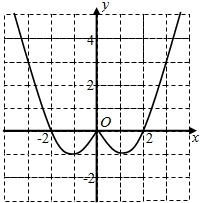
【答案】(1)图象详见解析,![]() 的递增区间是
的递增区间是![]() ,
,![]() ;(2)
;(2)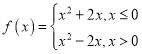 ,值域为
,值域为![]() .
.
【解析】
试题分析:(1)根据偶函数的图象关于![]() 轴对称的性质,可作出函数
轴对称的性质,可作出函数![]() 在
在![]() 轴左侧的图象,再根据函数
轴左侧的图象,再根据函数![]() 在
在![]() 上的图象,可得出函数的递增区间为
上的图象,可得出函数的递增区间为![]() 和
和![]() ;(2)由偶函数的性质
;(2)由偶函数的性质![]() ,取
,取![]() ,则
,则![]() ,
,![]() ,即
,即![]() ,从而可求得函数
,从而可求得函数![]() 的解析式,再根据图象,易求得函数的值域.
的解析式,再根据图象,易求得函数的值域.
试题解析:(1)因为函数为偶函数,故图象关于![]() 轴对称,补出完整函数图象如下图:
轴对称,补出完整函数图象如下图:
所以![]() 的递增区间是
的递增区间是![]() ,
,![]() .
.
(2)设![]() ,则
,则![]() ,所以
,所以![]() ,
,
因为![]() 是定义在
是定义在![]() 上的偶函数,所以
上的偶函数,所以![]() ,
,
所以![]() 时,
时,![]() ,
,
故![]() 的解析式为
的解析式为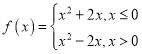 ,
,
值域为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 (a>b>0)的离心率
(a>b>0)的离心率 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论正确的是( )
A. 空间中不同三点确定一个平面
B. 空间中两两相交的三条直线确定一个平面
C. 一条直线和一个点能确定一个平面
D. 梯形一定是平面图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是奇函数.
是奇函数. (Ⅰ)求实数
 的值;
的值;(Ⅱ)用定义证明函数
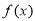 在
在 上的单调性;
上的单调性;(Ⅲ)若对任意的
 ,不等式
,不等式 恒成立,求实数
恒成立,求实数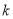 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, 为其导函数,且
为其导函数,且 时
时 有极小值-9.
有极小值-9.(1)求
 的单调递减区间;
的单调递减区间;(2)若
 ,
, ,当
,当 时,对于任意
时,对于任意 ,
, 和
和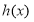 的值至少有一个是正数,求实数
的值至少有一个是正数,求实数 的取值范围;
的取值范围;(3)若不等式
 (
( 为正整数)对任意正实数
为正整数)对任意正实数 恒成立,求
恒成立,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
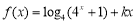 (
(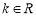 )是偶函数.
)是偶函数.(1)求k的值;
(2)若函数
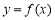 的图象与直线
的图象与直线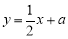 没有交点,求
没有交点,求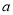 的取值范围;
的取值范围;(3)若函数
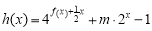 ,
, ,是否存在实数
,是否存在实数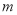 使得
使得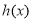 最小值为
最小值为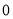 ,若存在,求出
,若存在,求出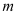 的值; 若不存在,请说明理由.
的值; 若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业为打入国际市场,决定从
 、
、 两种产品中只选择一种进行投资生产,已知投资生产这两种产品的有关数据如下表:(单位:万美元)
两种产品中只选择一种进行投资生产,已知投资生产这两种产品的有关数据如下表:(单位:万美元)年固定成本
每件产品成本
每件产品销售价
每年最多可生产的件数
A产品
20

10
200
B产品
40
8
18
120
其中年固定成本与年生产的件数无关,
 是待定常数,其值由生产
是待定常数,其值由生产 产品的原材料决定,预计
产品的原材料决定,预计 ,另外,年销售
,另外,年销售 件B产品时需上交
件B产品时需上交 万美元的特别关税,假设生产出来的产品都能在当年销售出去.
万美元的特别关税,假设生产出来的产品都能在当年销售出去.(1)求该厂分别投资生产A、
 两种产品的年利润
两种产品的年利润 与生产相应产品的件数
与生产相应产品的件数 之间的函数关系,并求出其定义域;
之间的函数关系,并求出其定义域;(2)如何投资才可获得最大年利润?请设计相关方案.
相关试题

