【题目】已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为![]() .
.
(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
参考答案:
【答案】(1)![]() ;(2)存在
;(2)存在![]()
【解析】
试题分析:(1)直线方程![]() 为:
为:![]()
![]()

![]()
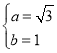
![]() 椭圆方程为
椭圆方程为 ![]() ;(2)假若存在这样的
;(2)假若存在这样的![]() 值,由
值,由
![]()
![]()
![]() .
.
![]()
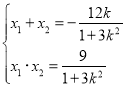
![]()
![]() .要使以
.要使以![]() 为直径的圆过点
为直径的圆过点![]()
![]() 当且仅当
当且仅当![]() 时
时![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 存在
存在![]() ,使得以
,使得以![]() 为直径的圆过点
为直径的圆过点![]() .
.
试题解析:(1)直线方程![]() 为:
为:![]() .
.
依题意 解得
解得 
∴ 椭圆方程为 ![]()
(2)假若存在这样的![]() 值,由
值,由 得
得![]()
![]() .
.
![]()
![]() . ①
. ①
设![]() ,
,![]() 、
、![]() ,
,![]() ,则
,则 ②
②
而![]() .
.
要使以![]() 为直径的圆过点
为直径的圆过点![]() ,当且仅当
,当且仅当![]() 时,则
时,则![]() ,即
,即![]() .
.
![]()
![]() . ③
. ③
将②式代入③整理解得![]() .经验证,
.经验证,![]() ,使①成立.
,使①成立.
综上可知,存在![]() ,使得以
,使得以![]() 为直径的圆过点
为直径的圆过点![]() .
.
-
科目: 来源: 题型:
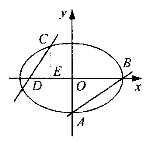
查看答案和解析>>【题目】已知方程
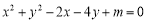 .
.(1)若此方程表示圆,求
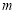 的取值范围;
的取值范围;(2)若(1)中的圆与直线
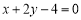 相交于
相交于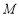 ,
,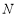 两点,且
两点,且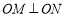 (
(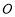 为坐标原点),求
为坐标原点),求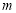 ;
;(3)在(2)的条件下,求以
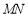 为直径的圆的方程.
为直径的圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】
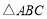 中,
中,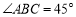 ,
,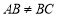 ,
,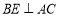 于点
于点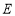 ,
,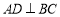 于点
于点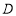 .
.(1)如图1,作
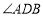 的角平分线
的角平分线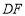 交
交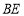 于点
于点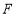 ,连接
,连接 .求证:
.求证: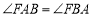 ;
;(2)如图2,连接
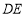 ,点
,点 与点
与点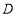 关于直线
关于直线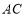 对称,连接
对称,连接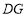 、
、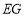 .
.
①依据题意补全图形;
②用等式表示线段
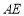 、
、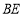 、
、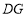 之间的数量关系,并加以证明.
之间的数量关系,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
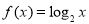 ,当点
,当点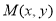 在
在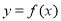 的图象上运动时,点
的图象上运动时,点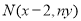 在函数
在函数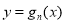 的图象上运动(
的图象上运动(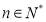 ).
).(Ⅰ)求
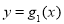 和
和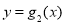 的表达式;
的表达式;(Ⅱ)已知关于
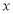 的方程
的方程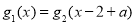 有实根,求实数
有实根,求实数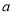 的取值范围;
的取值范围;(Ⅲ)设
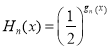 ,函数
,函数 的值域为
的值域为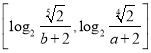 ,求实数
,求实数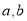 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论正确的是( )
A. 空间中不同三点确定一个平面
B. 空间中两两相交的三条直线确定一个平面
C. 一条直线和一个点能确定一个平面
D. 梯形一定是平面图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是奇函数.
是奇函数. (Ⅰ)求实数
 的值;
的值;(Ⅱ)用定义证明函数
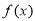 在
在 上的单调性;
上的单调性;(Ⅲ)若对任意的
 ,不等式
,不等式 恒成立,求实数
恒成立,求实数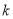 的取值范围.
的取值范围. -
科目: 来源: 题型:
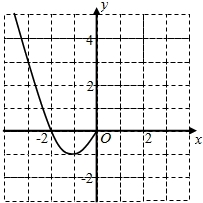
查看答案和解析>>【题目】已知函数是定义在上的偶函数,且当时,.
(1)现已画出函数在轴左侧的图象,如图所示,请补出完整函数的图象,并根据图象写出函数的增区间;
(2)写出函数的解析式和值域.
相关试题

