【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
 .
.
参考答案:
【答案】(1)![]() ;(2)二次函数回归模型更好,预测值为
;(2)二次函数回归模型更好,预测值为![]() 万元.
万元.
【解析】试题分析:(1)代入公式可求得![]() 的值,由此可得线性回归方程;(2)比较
的值,由此可得线性回归方程;(2)比较![]() 的值,可知二次函数回归模型更合适;将
的值,可知二次函数回归模型更合适;将![]() 代入二次函数回归模型可得销售额。
代入二次函数回归模型可得销售额。
试题解析:
(1)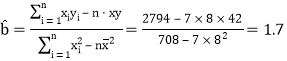
![]()
所以,![]() 关于
关于![]() 的线性回归方程是
的线性回归方程是![]()
(2)∵![]() ,∴二次函数回归模型更合适.
,∴二次函数回归模型更合适.
当![]() 万元时,预测
万元时,预测![]() 超市销售额为
超市销售额为![]() 万元.
万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(Ⅰ)当0≤x≤200时,求函数v(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
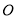 :
: 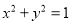 过椭圆
过椭圆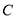 :
: 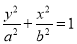 (
(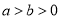 )的短轴端点,
)的短轴端点, 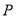 ,
, 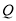 分别是圆
分别是圆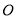 与椭圆
与椭圆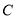 上任意两点,且线段
上任意两点,且线段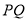 长度的最大值为3.
长度的最大值为3.(Ⅰ)求椭圆
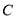 的方程;
的方程;(Ⅱ)过点
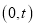 作圆
作圆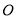 的一条切线交椭圆
的一条切线交椭圆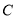 于
于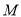 ,
, 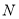 两点,求
两点,求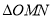 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
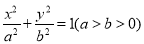 的离心率
的离心率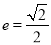 ,左顶点为
,左顶点为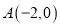 .
.(1)求椭圆
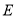 的方程;
的方程; (2)已知
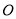 为坐标原点,
为坐标原点, 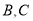 是椭圆
是椭圆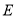 上的两点,连接
上的两点,连接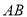 的直线平行
的直线平行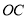 交
交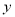 轴于点
轴于点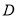 ,证明:
,证明: 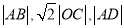 成等比数列.
成等比数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
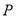 为抛物线
为抛物线 上一个动点,
上一个动点,  为圆
为圆 上一个动点,那么点
上一个动点,那么点 到点
到点 的距离与点
的距离与点 到抛物线的准线距离之和的最小值是( )
到抛物线的准线距离之和的最小值是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
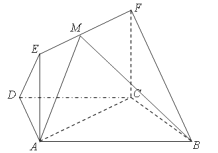
查看答案和解析>>【题目】如图,在梯形
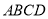 中,
中, 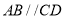 ,
,  ,
, 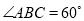 ,四边形
,四边形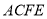 为矩形,平面
为矩形,平面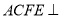 平面
平面 ,
, 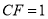 .
.
(1)求证:
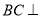 平面
平面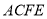 ;
;(2)点
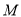 在线段
在线段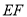 上运动,设平面
上运动,设平面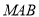 与平面
与平面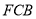 所成二面角的平面角为
所成二面角的平面角为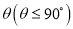 ,试求
,试求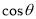 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为
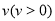 ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为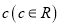 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与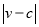 ×S成正比,比例系数为
×S成正比,比例系数为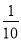 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为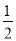 ,记
,记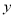 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=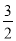 时。
时。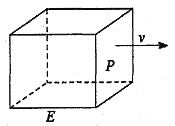
(1)写出
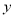 的表达式
的表达式(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度
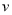 ,使总淋雨量
,使总淋雨量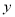 最少。
最少。
相关试题

