【题目】已知不等式![]() 对一切
对一切![]() 都成立,则
都成立,则![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
参考答案:
【答案】C
【解析】令![]() ,则
,则![]()
若a≤0,则y′>0恒成立,x>﹣1时函数递增,无最值.
若a>0,由y′=0得:x=![]() ,
,
当﹣1<x<![]() 时,y′>0,函数递增;
时,y′>0,函数递增;
当x>![]() 时,y′<0,函数递减.
时,y′<0,函数递减.
则x=![]() 处取得极大值,也为最大值﹣lna+a﹣b﹣2,
处取得极大值,也为最大值﹣lna+a﹣b﹣2,
∴﹣lna+a﹣b﹣2≤0,
∴b≥﹣lna+a﹣2,
∴![]() ≥1﹣
≥1﹣![]() ﹣
﹣![]() ,
,
令t=1﹣![]() ﹣
﹣![]() ,
,
∴t′=![]() ,
,
∴(0,e﹣1)上,t′<0,(e﹣1,+∞)上,t′>0,
∴a=e﹣1,tmin=1﹣e.
∴![]() 的最小值为1﹣e.
的最小值为1﹣e.
点晴:本题主要考查用导数研究不等式恒成立问题. 解决这类问题的一种方法法是:通过变量分离将含参函数的问题转化为不含参的确定函数的最值问题,本题中a≤0时,则y′>0恒成立,x>﹣1时函数递增,无最值.a>0时x=![]() 处取得极大值,也为最大值﹣lna+a﹣b﹣2≤0,可得b≥﹣lna+a﹣2,于是
处取得极大值,也为最大值﹣lna+a﹣b﹣2≤0,可得b≥﹣lna+a﹣2,于是![]() ≥1﹣
≥1﹣![]() ﹣
﹣![]() ,令t=1﹣
,令t=1﹣![]() ﹣
﹣![]() ,然后利用导数研究这个函数的单调性、极值和最值,可得
,然后利用导数研究这个函数的单调性、极值和最值,可得![]() 的最小值.
的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
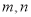 是空间两条直线,
是空间两条直线, 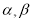 是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )A. 当
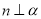 时,“
时,“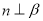 ”是“
”是“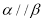 ”的充要条件
”的充要条件B. 当
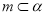 时,“
时,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件C. 当
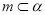 时,“
时,“ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件D. 当
 时,“
时,“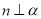 ”是“
”是“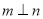 ”的充分不必要条件
”的充分不必要条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,
中,  底面
底面 ,
,  ,
,  ,
,  ,
,  分别是
分别是 ,
, 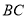 的中点,
的中点,  在
在 上,且
上,且 .
.(1)求证:
 平面
平面 ;
;(2)在线段上
 上是否存在点
上是否存在点 ,使二面角
,使二面角 的大小为
的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
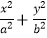 =1(a>b>0)过点A(2,0),B(0,1)两点.
=1(a>b>0)过点A(2,0),B(0,1)两点.
(1)求椭圆C的方程及离心率;
(2)设直线l与椭圆相交于不同的两点A,B.已知点A的坐标为(﹣a,0),点 Q(0,y0)在线段AB的垂直平分线上,且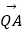
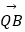 =4,求y0的值.
=4,求y0的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
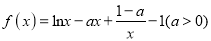
(1)设
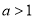 ,试讨论
,试讨论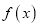 单调性;
单调性;(2)设
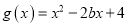 ,当
,当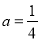 时,任意
时,任意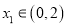 ,存在
,存在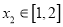 ,使
,使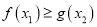 ,求实数
,求实数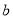 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知中心在原点,焦点在
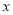 轴上的椭圆的一个焦点为
轴上的椭圆的一个焦点为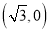 ,
, 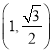 是椭圆上的一个点.
是椭圆上的一个点.(1)求椭圆的标准方程;
(2)设椭圆的上、下顶点分别为
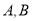 ,
, 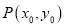 (
(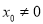 )是椭圆上异于
)是椭圆上异于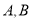 的任意一点,
的任意一点, 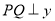 轴,
轴, 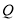 为垂足,
为垂足, 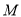 为线段
为线段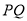 中点,直线
中点,直线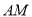 交直线
交直线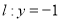 于点
于点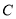 ,
, 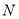 为线段
为线段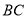 的中点,如果
的中点,如果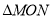 的面积为
的面积为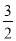 ,求
,求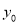 的值.
的值.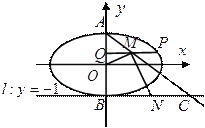
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的最小正周期为π,若其图象向左平移
的最小正周期为π,若其图象向左平移  个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点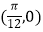 对称
对称
B.关于点 对称
对称
C.关于直线 对称
对称
D.关于直线 对称
对称
相关试题

