【题目】已知函数![]()
(I)若![]() ,求函数
,求函数![]() 的极值和单调区间;
的极值和单调区间;
(II)若在区间![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(I)![]() 时,
时,![]() 的极小值为1;单调递增区间为
的极小值为1;单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(II)
;(II)![]() .
.
【解析】
试题(I)首先求出导函数,然后令导数等于零,解方程,从而根据定义域列表讨论,求得函数![]() 的单调区间和极值;(II)首先根据题意将问题转化为
的单调区间和极值;(II)首先根据题意将问题转化为![]() 在区间
在区间![]() 上的最小值小于0即可,从而首先求出导函数
上的最小值小于0即可,从而首先求出导函数![]() ,然后分
,然后分![]() 、
、![]() 研究函数在
研究函数在![]() 上的单调性,将
上的单调性,将![]() 的各极值与其端点的函数值比较,其中最小的一个就是最小值,进而求得
的各极值与其端点的函数值比较,其中最小的一个就是最小值,进而求得![]() 的取值范围.
的取值范围.
试题解析:(I)因为![]() ,
,
当![]() ,
,![]() .
.
令![]() ,得
,得![]() .
.
又![]() 的定义域为
的定义域为![]() ,
,![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
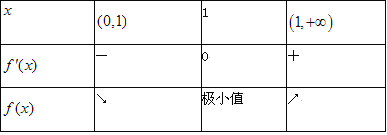
所以![]() 时,
时,![]() 的极小值为1.
的极小值为1.
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(II)因为![]() ,且
,且![]() ,
,
令![]() ,得到
,得到![]() .
.
若在区间![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,
成立,
其充要条件是![]() 在区间
在区间![]() 上的最小值小于0即可.
上的最小值小于0即可.
(1)当![]() 时,
时,![]() 对
对![]() 成立,
成立,
所以,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
故![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,得
,得![]() ,即
,即![]()
(2)当![]() 时,
时,
①若![]() ,则
,则![]() 对
对![]() 成立,
成立,
所以![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以,![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
显然,![]() 在区间
在区间![]() 上的最小值小于0不成立
上的最小值小于0不成立
②若![]() ,即
,即![]() 时,则有
时,则有
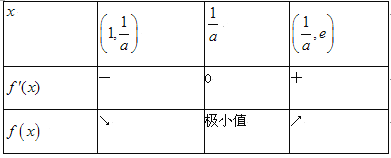
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,
,
得![]() ,解得
,解得![]() ,即
,即![]() 舍去;
舍去;
当![]() ,即
,即![]() ,即有
,即有![]() 在
在![]() 递增,
递增,
可得![]() 取得最小值,且为1,
取得最小值,且为1,![]() ,不成立.
,不成立.
综上,由(1)(2)可知![]() 符合题意.
符合题意.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
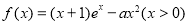 .
.(1)若函数
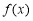 在
在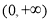 上单调递增,求实数
上单调递增,求实数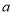 的取值范围;
的取值范围;(2)若函数
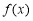 有两个不同的零点
有两个不同的零点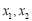 .
.(ⅰ)求实数
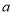 的取值范围;
的取值范围;(ⅱ)求证:
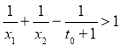 .(其中
.(其中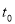 为
为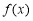 的极小值点)
的极小值点) -
科目: 来源: 题型:
查看答案和解析>>【题目】对于某种类型的口服药,口服
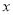 小时后,由消化系统进入血液中药物浓度
小时后,由消化系统进入血液中药物浓度 (单位)与时间
(单位)与时间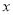 小时的关系为
小时的关系为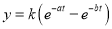 ,其中
,其中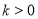 ,
,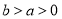 为常数,对于某一种药物
为常数,对于某一种药物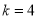 ,
,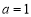 ,
,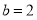 .
.(1)口服药物后______小时血液中药物浓度最高;
(2)这种药物服药
 小时后血液中药物浓度如下表
小时后血液中药物浓度如下表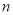
1
2
3
4
5
6
7
8
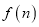
0.9545
0.9304
0.6932
0.4680
0.3010
0.1892
0.1163
0.072
一个病人上午8:00第一次服药,要使得病人血液中药物浓度保持在0.5个单位以上,第三次服药时间是______(时间以整点为准)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点
 在正视图上的对应点为
在正视图上的对应点为 ,圆柱表面上的点
,圆柱表面上的点 在左视图上的对应点为
在左视图上的对应点为 ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从 到
到 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )
A.
 B.
B.  C.
C.  D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1,  ),P4(1,
),P4(1,  )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】刍甍,中国古代算术中的一种几何图形,《九章算术》中记载“刍甍者,下有褒有广,而上有褒无广”刍,草也;甍,屋盖也.翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱,刍甍字面意思为茅草屋顶”如图,为一刍甍的三视图,其中正视图为等腰梯形,侧视图为等腰三角形,若用茅草搭建它(无底面,不考虑厚度),则需要覆盖的面积至少为( )



A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,四边形ABCD为平行四边形,且
中,四边形ABCD为平行四边形,且 ,
, ,
, 平面PAC.
平面PAC.
(1)求证:
 平面
平面 ;
;(2)若异面直线PC与AD所成的角为30°,求二面角
 的余弦值.
的余弦值.
相关试题

