【题目】刍甍,中国古代算术中的一种几何图形,《九章算术》中记载“刍甍者,下有褒有广,而上有褒无广”刍,草也;甍,屋盖也.翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱,刍甍字面意思为茅草屋顶”如图,为一刍甍的三视图,其中正视图为等腰梯形,侧视图为等腰三角形,若用茅草搭建它(无底面,不考虑厚度),则需要覆盖的面积至少为( )



A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】A
【解析】
由三视图可知该刍甍是一个组合体,它由成一个直三棱柱和两个全等的四棱锥组成,根据三视图中的数据可得其需要覆盖的面积.
根据三视图画出其立体图形:如图
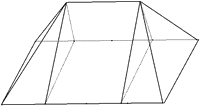
茅草覆盖面积即为几何体的侧面积,
根据立体图形可知该几何体的侧面为两个全等的等腰梯形和两个全等的等腰三角形.
其中,等腰梯形的上底长为![]() ,下底长为
,下底长为![]() ,高为
,高为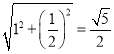 ;
;
等腰三角形的底边长为![]() ,高为
,高为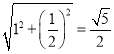 .
.
故侧面积为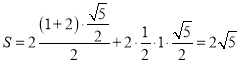 .
.
即需要茅草覆盖面积至少为![]() ,
,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点
 在正视图上的对应点为
在正视图上的对应点为 ,圆柱表面上的点
,圆柱表面上的点 在左视图上的对应点为
在左视图上的对应点为 ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从 到
到 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )
A.
 B.
B.  C.
C.  D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
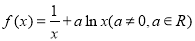
(I)若
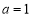 ,求函数
,求函数 的极值和单调区间;
的极值和单调区间;(II)若在区间
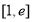 上至少存在一点
上至少存在一点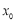 ,使得
,使得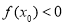 成立,求实数
成立,求实数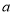 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1,  ),P4(1,
),P4(1,  )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,四边形ABCD为平行四边形,且
中,四边形ABCD为平行四边形,且 ,
, ,
, 平面PAC.
平面PAC.
(1)求证:
 平面
平面 ;
;(2)若异面直线PC与AD所成的角为30°,求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
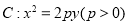 的焦点为F,A为C上异于原点的任意一点,过点A的直线交y轴正半轴于点B,且有
的焦点为F,A为C上异于原点的任意一点,过点A的直线交y轴正半轴于点B,且有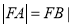 ,当点A的纵坐标为6时,
,当点A的纵坐标为6时,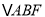 为正三角形.
为正三角形.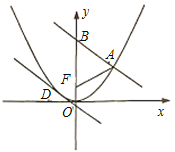
(1)求C的方程;
(2)若直线
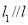 ,且
,且 和C有且只有一个公共点D,证明:直线AD过定点,并求出该定点坐标.
和C有且只有一个公共点D,证明:直线AD过定点,并求出该定点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】笔、墨、纸、砚是中国独有的文书工具,即文房四宝.笔、墨、纸、砚之名,起源于南北朝时期,其中“纸”指的是宣纸,“始于唐代,产于泾县”,因唐代泾县隶属宣州管辖,故因地得名宣纸,宣纸按质量等级分类可分为正牌和副牌(优等品和合格品)某公司生产的宣纸为纯手工制作,年产宣纸10000刀,该公司按照某种质量指标x给宣纸确定质量等级,如下表所示:
x的范围
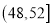
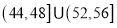
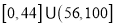
质量等级
正牌
副牌
废品
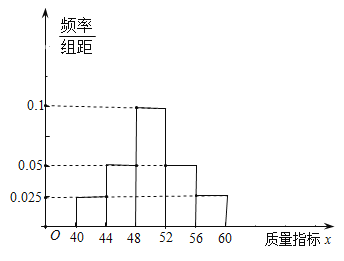
公司在所生产的宣纸中随机抽取了一刀(100张)进行检验,得到的频率分布直方图如上图所示.已知每张正牌宣纸的利润为12元,副牌宣纸的利润为6元,废品宣纸的利润为-12元.
(1)试估计该公司生产宣纸的利润;
(2)该公司预备购买一种售价为100万元的机器改进生产工艺,这种机器使用寿命为一年,不影响产量,这种机器生产的宣纸的质量指标x服从正态分布
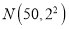 ,改进工艺后正牌和副牌宣纸的利润都将受到不同程度的影响,观测的数据如下表所示:
,改进工艺后正牌和副牌宣纸的利润都将受到不同程度的影响,观测的数据如下表所示:x的范围
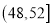
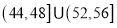
一张宣纸的利润
12
8
8
3
频率
0.5
0.5
0.5
0.5
将频率视为概率,请判断该公司是否应该购买这种机器,并说明理由
. 附:若
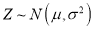 ,则
,则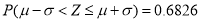 ,
,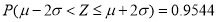 ,
,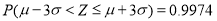 .
.
相关试题

