【题目】平面直角坐标系xoy中,直线l的参数方程是 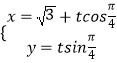 (t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是
(t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是 ![]() +ρ2sin2θ=1.
+ρ2sin2θ=1.
(1)求曲线C的直角坐标方程;
(2)求直线l与曲线C相交所得的弦AB的长.
参考答案:
【答案】
(1)解:曲线C的极坐标方程是 ![]() +ρ2sin2θ=1,把x=ρcosθ,y=ρsinθ代入可得:
+ρ2sin2θ=1,把x=ρcosθ,y=ρsinθ代入可得: ![]() =1
=1
(2)解:直线l的参数方程是 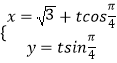 (t为参数),即
(t为参数),即 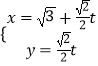 ,代入椭圆方程可得:
,代入椭圆方程可得: ![]() ﹣2=0,
﹣2=0,
∴t1+t2= ![]() ,t1t2=﹣
,t1t2=﹣ ![]() ,∴|AB|=|t1﹣t2|=
,∴|AB|=|t1﹣t2|= ![]() =
=  =
= ![]()
【解析】(1)曲线C的极坐标方程是 ![]() +ρ2sin2θ=1,把x=ρcosθ,y=ρsinθ代入可得直角坐标方程..(2)直线l的参数方程是
+ρ2sin2θ=1,把x=ρcosθ,y=ρsinθ代入可得直角坐标方程..(2)直线l的参数方程是 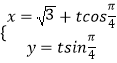 (t为参数),即
(t为参数),即 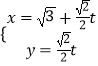 ,代入椭圆方程可得:
,代入椭圆方程可得: ![]() ﹣2=0,利用|AB|=|t1﹣t2|=
﹣2=0,利用|AB|=|t1﹣t2|= ![]() 即可得出.
即可得出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市拟兴建九座高架桥,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
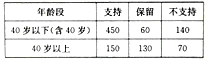
(1)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在40岁以下(含40岁)的人有多少被抽取;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在40岁以上的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 定义域为
定义域为 ,对任意
,对任意 都有
都有 ,且当
,且当 时,
时,  .
.(1)试判断
 的单调性,并证明;
的单调性,并证明;(2)若
 ,
,①求
 的值;
的值;②求实数
 的取值范围,使得方程
的取值范围,使得方程 有负实数根.
有负实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】信息科技的进步和互联网商业模式的兴起,全方位地改变了大家金融消费的习惯和金融交易模式,现在银行的大部分业务都可以通过智能终端设备完成,多家银行职员人数在悄然减少.某银行现有职员320人,平均每人每年可创利20万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.2万元,但银行需付下岗职员每人每年6万元的生活费,并且该银行正常运转所需人数不得小于现有职员的
 ,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以原点为极点,
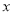 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线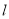 的极坐标方程为
的极坐标方程为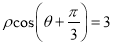 ,曲线
,曲线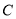 的极坐标方程为
的极坐标方程为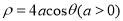 .
.(1)设
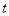 为参数,若
为参数,若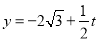 ,求直线
,求直线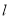 的参数方程;
的参数方程;(2)已知直线
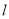 与曲线
与曲线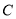 交于
交于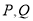 ,设
,设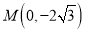 ,且
,且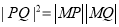 ,求实数
,求实数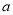 的值.
的值. -
科目: 来源: 题型:
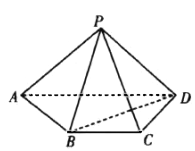
查看答案和解析>>【题目】如图,已知四棱锥
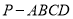 的底面为直角梯形,
的底面为直角梯形, 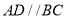 ,
, 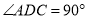 ,且
,且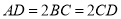 ,
, 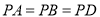 .
.
(1)求证:平面
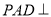 平面
平面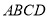 ;
;(2)设
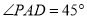 ,求二面角
,求二面角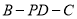 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
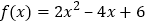
(1)设函数
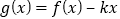 ,且函数
,且函数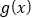 在区间
在区间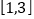 上是单调函数,求实数
上是单调函数,求实数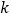 的取值范围;
的取值范围;(2)设函数
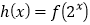 ,求当
,求当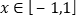 时,函数
时,函数 的值域。
的值域。
相关试题

