【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,设
,设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
参考答案:
【答案】(1) 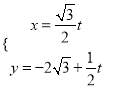 (
(![]() 为参数);(2)
为参数);(2) ![]() .
.
【解析】试题分析:(1)利用直线极坐标方程和直角坐标方程互化的公式,先得直角坐标方程,再根据![]() ,即可求直线l参数方程;(2)把直线l的参数方程代入曲线C的方程,设MP=t1,MQ=t2.根据|PQ|2=|MP||MQ|,
,即可求直线l参数方程;(2)把直线l的参数方程代入曲线C的方程,设MP=t1,MQ=t2.根据|PQ|2=|MP||MQ|, ![]() 根据根与系数的关系即可得出.
根据根与系数的关系即可得出.
解析:(1)直线![]() 的极坐标方程为
的极坐标方程为![]()
所以![]() ,即
,即![]()
因为![]() 为参数,若
为参数,若![]() ,代入上式得
,代入上式得![]() ,
,
所以直线![]() 的参数方程为
的参数方程为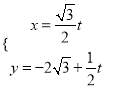 (
(![]() 为参数)
为参数)
(2)由![]() ,得
,得![]()
由![]() 代入,得
代入,得![]()
将直线![]() 的参数方程与
的参数方程与![]() 的直角坐标方程联立
的直角坐标方程联立
得![]() (*)
(*)
![]()
![]() ,
,
设点![]() 分别对应参数
分别对应参数![]() 恰为上述方程的根
恰为上述方程的根
则![]() ,
,
由题设得![]() ,
,
则有![]() ,得
,得![]() 或
或![]()
因为![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列{an}满足
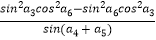 =1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
=1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
A.(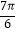 ,
, 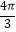 )
)
B.[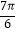 ,
, 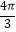 ]
]
C.(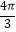 ,
, 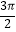 )
)
D.[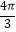 ,
, 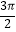 ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
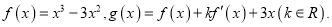
(1)讨论
 的单调性;
的单调性;(2)若直线
 与曲线
与曲线 都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积.
都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果右边程序执行后输出的结果是132,那么在程序until后面的“条件”应为( )

A.i > 11
B.i ≥11
C.i ≤11
D.i<11 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列满足:a1=1,an+1=
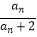 ,(n∈N*),若bn+1=(n﹣λ)(
,(n∈N*),若bn+1=(n﹣λ)( 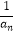 +1),b1=﹣λ,且数列{bn}是单调递增数列,则实数λ的取值范围为 .
+1),b1=﹣λ,且数列{bn}是单调递增数列,则实数λ的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】右边程序执行后输出的结果是( )

A.-1
B.0
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知公差不为零的等差数列{an}中,a1=1,且a1 , a3 , a9成等比数列.
(1)求数列{an}的通项公式;
(2)设bn= +n,求数列Sn的前Sn项和Sn .
+n,求数列Sn的前Sn项和Sn .
相关试题

