搜索
【题目】设f（x）=|lnx|，若函数g（x）=f（x）﹣ax在区间（0，3]上有三个零点，则实数a的取值范围是（ ）
A.（0， 
）
B.（ 
，e）
C.（0， ]
D.[ ， ）
参考答案：
【答案】D
【解析】解：函数f（x）=|lnx|的图象如图示：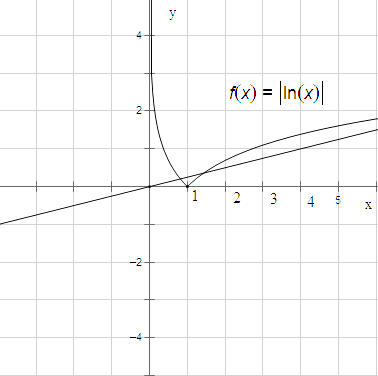 
当a≤0时，显然，不合乎题意，
当a＞0时，如图示，
当x∈（0，1]时，存在一个零点，
当x＞1时，f（x）=lnx，
可得g（x）=lnx﹣ax，（x∈（1，3]）
g′（x）= 
= 
，
若g′（x）＜0，可得x＞ 
，g（x）为减函数，
若g′（x）＞0，可得x＜ ，g（x）为增函数，
此时f（x）必须在[1，3]上有两个零点，
∴ 
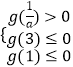
解得， 
，
在区间（0，3]上有三个零点时， ，
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设a，b∈R，且a≠2，定义在区间（﹣b，b）内的函数f（x）=lg
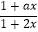是奇函数．
（1）求a的值；
（2）求b的取值范围；
（3）用定义讨论并证明函数f（x）的单调性． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知两条直线l1：y=a和l2：y=
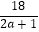（其中a＞0），若直线l1与函数y=|log4x|的图象从左到右相交于点A，B，直线l2与函数y=|log4x|的图象从左到右相交于点C，D．记线段AC和BD在x轴上的投影长度分别为 m，n．令f（a）=log4 
．
（1）求f（a）的表达式；
（2）当a变化时，求出f（a）的最小值，并指出取得最小值时对应的a的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆
(a>b>0)的左、右焦点分别为F1，F2，点M(0，2)是椭圆的一个顶点，△F1MF2是等腰直角三角形．(1)求椭圆的方程；
(2)过点M分别作直线MA，MB交椭圆于A，B两点，设两直线的斜率分别为k1，k2，且k1＋k2＝8，证明：直线AB过定点
. -
科目： 来源： 题型：
查看答案和解析>>【题目】若函数f（x）为定义在R上的奇函数，且在（0，+∞）内是增函数，又f（2）=0，则不等式x5f（x）＞0的解集为（ ）
A.（﹣2，0）∪（2，+∞）
B.（﹣∞，﹣2）∪（0，2）
C.（﹣2，0）∪（0，2）
D.（﹣∞，﹣2）∪（2，+∞） -
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中，正确的是
·（1）任取x＞0，均有3x＞2x；
·（2）当a＞0，且a≠1时，有a3＞a2；
·（3）y=（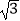
）﹣x是减函数；
·（4）函数f（x）在x＞0时是增函数，x＜0也是增函数，所以f（x）是增函数；
·（5）若函数f（x）=ax2+bx+2与x轴没有交点，则b2﹣8a＜0且a＞0；
·（6）y=x2﹣2|x|﹣3的递增区间为[1，+∞）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，椭圆C：
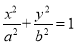(a＞b＞0)的离心率为
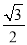，其左焦点到点
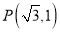的距离为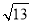
．不过原点O的直线
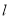与C相交于A，B两点，且线段AB被直线OP平分．（1）求椭圆C的方程；
（2）求
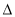ABP的面积取最大时直线l的方程．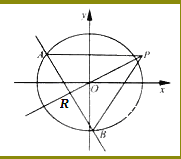
相关试题
