【题目】已知两条直线l1:y=a和l2:y= ![]() (其中a>0),若直线l1与函数y=|log4x|的图象从左到右相交于点A,B,直线l2与函数y=|log4x|的图象从左到右相交于点C,D.记线段AC和BD在x轴上的投影长度分别为 m,n.令f(a)=log4
(其中a>0),若直线l1与函数y=|log4x|的图象从左到右相交于点A,B,直线l2与函数y=|log4x|的图象从左到右相交于点C,D.记线段AC和BD在x轴上的投影长度分别为 m,n.令f(a)=log4 ![]() .
.
(1)求f(a)的表达式;
(2)当a变化时,求出f(a)的最小值,并指出取得最小值时对应的a的值.
参考答案:
【答案】
(1)
解:设A(xA,yA),B(xB,yB),C(xC,yC),D(xD,yD),
则 ![]() ,
,
则  ∴
∴ ![]()
(2)
解: ![]() ,∵a
,∵a ![]() >
> ![]() ,∴f(a)≥2
,∴f(a)≥2 ![]() ﹣
﹣ ![]() =
= ![]() .当且仅当a
.当且仅当a ![]() =
= ![]() 即a=
即a= ![]() 时取等号.
时取等号.
所以当 ![]() 时f(a)取得最小值
时f(a)取得最小值 ![]()
【解析】(1)用a表示出A,B,C,D四点的横坐标,计算 ![]() 的值,(2)使用基本不等式解出f(a)的最小值.
的值,(2)使用基本不等式解出f(a)的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=x2+2ax﹣a﹣1,x∈[0,2],a为常数.
(1)求f(x)的最小值g(a)的解析式;
(2)在(1)中,是否存在最小的整数m,使得g(a)﹣m≤0对于任意a∈R均成立,若存在,求出m的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】有人发现,多看电视容易使人变冷漠,如表是一个调查机构对此现象的调查结果:
冷漠
不冷漠
总计
多看电视
68
42
110
少看电视
20
38
58
总计
88
80
168
P(K2≥k)
0.025
0.010
0.005
0.001
k
5.024
6.635
7.879
10.828
K2=
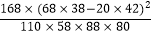 ≈11.377,下列说法正确的是( )
≈11.377,下列说法正确的是( )
A.大约有99.9%的把握认为“多看电视与人变冷漠”有关系
B.大约有99.9%的把握认为“多看电视与人变冷漠”没有关系
C.某人爱看电视,则他变冷漠的可能性为99.9%
D.爱看电视的人中大约有99.9%会变冷漠 -
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b∈R,且a≠2,定义在区间(﹣b,b)内的函数f(x)=lg
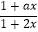 是奇函数.
是奇函数.
(1)求a的值;
(2)求b的取值范围;
(3)用定义讨论并证明函数f(x)的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 (a>b>0)的左、右焦点分别为F1,F2,点M(0,2)是椭圆的一个顶点,△F1MF2是等腰直角三角形.
(a>b>0)的左、右焦点分别为F1,F2,点M(0,2)是椭圆的一个顶点,△F1MF2是等腰直角三角形.(1)求椭圆的方程;
(2)过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=8,证明:直线AB过定点
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=|lnx|,若函数g(x)=f(x)﹣ax在区间(0,3]上有三个零点,则实数a的取值范围是( )
A.(0,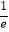 )
)
B.(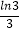 ,e)
,e)
C.(0,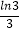 ]
]
D.[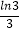 ,
, 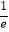 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)为定义在R上的奇函数,且在(0,+∞)内是增函数,又f(2)=0,则不等式x5f(x)>0的解集为( )
A.(﹣2,0)∪(2,+∞)
B.(﹣∞,﹣2)∪(0,2)
C.(﹣2,0)∪(0,2)
D.(﹣∞,﹣2)∪(2,+∞)
相关试题

