【题目】为迎接2022年北京冬季奥运会, 某校开设了冰球选修课,12名学生被分成甲、乙两组进行训练.他们的身高(单位:cm)如下图所示:

设两组队员身高平均数依次为![]() ,
,![]() ,方差依次为
,方差依次为![]() ,
,![]() ,则下列关系式中完全正确的是( )
,则下列关系式中完全正确的是( )
A. ![]() =
=![]() ,
, ![]() =
=![]() B.
B. ![]() <
<![]() ,
,![]() >
>![]()
C. ![]() <
<![]() ,
,![]() =
=![]() D.
D. ![]() <
<![]() ,
,![]() <
<![]()
参考答案:
【答案】C
【解析】
由茎叶图,分别求出两组数据的平均数和方差,由此能求出结果.
解:由茎叶图,得:
![]() (174+175+176+177+178+179)=176.5,
(174+175+176+177+178+179)=176.5,
![]() [(174﹣176.5)2+(175﹣176.5)2+(176﹣176.5)2+(177﹣176.5)2+(178﹣176.5)2+(179﹣176.5)2]=
[(174﹣176.5)2+(175﹣176.5)2+(176﹣176.5)2+(177﹣176.5)2+(178﹣176.5)2+(179﹣176.5)2]=![]() ,
,
![]() (176+177+178+179+180+181)=178.5,
(176+177+178+179+180+181)=178.5,
![]() [(176﹣178.5)2+(177﹣178.5)2+(178﹣178.5)2+(179﹣178.5)2+(180﹣178.5)2+(181﹣178.5)2]=
[(176﹣178.5)2+(177﹣178.5)2+(178﹣178.5)2+(179﹣178.5)2+(180﹣178.5)2+(181﹣178.5)2]=![]() ,.
,.
∴![]() <
<![]() ,
,![]() =
=![]() .
.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接夏季旅游旺季的到来,少林寺单独设置了一个专门安排游客住宿的客栈,寺庙的工作人员发现为游客准备的一些食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份入住客栈的游客约为100人,随后逐月递增直到8月份达到最多.
(1)试用一个正弦型三角函数
 描述一年中入住客栈的游客人数y与月x份之间的关系;
描述一年中入住客栈的游客人数y与月x份之间的关系;(2)请问哪几个月份要准备400份以上的食物?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将一矩形花坛
 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 点在
点在 上,
上, 点在
点在 上,且对角线
上,且对角线 过
过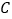 点,已知
点,已知 米,
米, 米.
米.
(1)要使矩形
 的面积大于
的面积大于 平方米,则
平方米,则 的长应在什么范围内?
的长应在什么范围内?(2)当
 的长度是多少时,矩形花坛
的长度是多少时,矩形花坛 的面积最小?并求出最小值.
的面积最小?并求出最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(
 ,
, )
)C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
 (b>0)的左、右焦点分别为
(b>0)的左、右焦点分别为 ,其一条渐近线方程为y=
,其一条渐近线方程为y= x,点P在该双曲线上,且
x,点P在该双曲线上,且 ,则
,则 =( )
=( )A. 4 B. 4
 C. 8 D.
C. 8 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=
 ,∠EAD=∠EAB.
,∠EAD=∠EAB. 
(1)证明:平面ACEF⊥平面ABCD;
(2)若AE与平面ABCD所成角为60°,求二面角B﹣EF﹣D的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司制造两种电子设备:影片播放器和音乐播放器.在每天生产结束后,要对产品进行检测,故障的播放器会被移除进行修复. 下表显示各播放器每天制造的平均数量以及平均故障率.
商品类型
播放器每天平均产量
播放器每天平均故障率
影片播放器
3000
4%
音乐播放器
9000
3%
下面是关于公司每天生产量的叙述:
①每天生产的播放器有三分之一是影片播放器;
②在任何一批数量为100的影片播放器中,恰好有4个会是故障的;
③如果从每天生产的音乐播放器中随机选取一个进行检测,此产品需要进行修复的概率是0.03.
上面叙述正确的是___________.
相关试题

