【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出和收益情况,如表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y关于x的线性回归方程;
(2)预测售出8箱水的收益是多少元?
附:回归直线的最小二乘法估计公式分别为:![]() =
=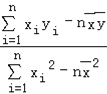 ,
,![]() =
=![]() ﹣
﹣![]()
![]() ,
,
参考答案:
【答案】(1) ![]() (2)186
(2)186
【解析】试题分析:(Ⅰ)首先求出![]() 的平均数,得到样本中心点,利用最小二乘法求出线性回归方程的系数,即可写出线性回归方程.
的平均数,得到样本中心点,利用最小二乘法求出线性回归方程的系数,即可写出线性回归方程.
(Ⅱ)当自变量取8时,把8代入线性回归方程,求出销售额的预报值.
试题解析:((1) 由所给数据计算得![]() =
=![]() (7+6+6+5+6)=6,
(7+6+6+5+6)=6,
![]() =
=![]() =146,
=146,
![]()
![]() =72+62+62+52+62=182,
=72+62+62+52+62=182,
![]() =
=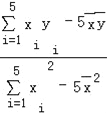 =
=![]() =20,
=20,
![]() =
=![]() ﹣
﹣![]()
![]() =146﹣20×6=26,
=146﹣20×6=26,
所求回归直线方程为![]() =20x+26;
=20x+26;
(2)将x=8代入回归方程可预测售出8箱水的收益为
![]() =20×8+26=186(元).
=20×8+26=186(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校100名学生期中考试数学成绩的频率分布直方图如图:
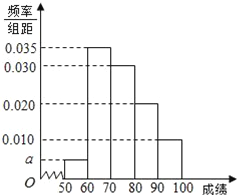
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (其中
(其中 为自然对数的底数)
为自然对数的底数)(1)设过点
 的直线
的直线 与曲线
与曲线 相切于点
相切于点 ,求
,求 的值;
的值;(2)函数
 的的导函数为
的的导函数为 ,若
,若 在
在 上恰有两个零点,求
上恰有两个零点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,只是告诉大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”.
(1)求乙班总分超过甲班的概率;
(2)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分.若主持人从甲乙两班所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为
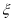 ,求
,求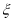 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=sin(2ωx+φ)(ω>0,0<φ<π)的最小正周期为π,且函数图象关于点(﹣
 ,0)对称,则函数的解析式为( )
,0)对称,则函数的解析式为( )
A.y=sin(4x+ )
)
B.y=sin(2x+ )
)
C.y=sin(2x+ )
)
D.y=sin(4x+ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)在定义域上存在区间[a,b](ab>0),使f(x)在[a,b]上值域为[
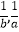 ],则称f(x)在[a,b]上具有“反衬性”.下列函数①f(x)=﹣x+
],则称f(x)在[a,b]上具有“反衬性”.下列函数①f(x)=﹣x+  ②f(x)=﹣x2+4x ③f(x)=sin
②f(x)=﹣x2+4x ③f(x)=sin  x ④f(x)=
x ④f(x)= 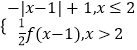 ,具有“反衬性”的为|( )
,具有“反衬性”的为|( )
A.②③
B.①③
C.①④
D.②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=1,AD=
 ,P矩形内的一点,且AP=
,P矩形内的一点,且AP= 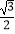 ,若
,若 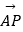 =λ
=λ 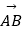 +μ
+μ 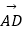 ,(λ,μ∈R),則λ+
,(λ,μ∈R),則λ+  μ的最大值为 .
μ的最大值为 . 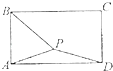
相关试题

