【题目】中国古代算书《孙子算经》中有一著名的问题“物不知数”如图1,原题为:今有物,不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?后来,南宋数学家秦九韶在其著作《数学九章》中对此类问题的解法做了系统的论述,并称之为“大衍求一术”,如图2程序框图的算法思路源于“大衍求一术”执行该程序框图,若输入的a,b分别为20,17,则输出的c=( )
A.1
B.6
C.7
D.11
参考答案:
【答案】C
【解析】解:模拟执行程序运行过程,如下;
a=20,b=17,r=3,c=1,m=0,n=1,满足r≠1;
a=17,b=3,r=2,q=5,m=1,n=1,c=6,满足r≠1;
a=3,b=2,r=1,q=1,m=1,n=6,c=7,满足r=1;
输出c=7.
故选:C.
模拟执行程序运行过程,即可得出程序运行后输出的c值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
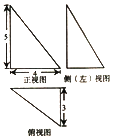
A.200π
B.50π
C.100π
D. π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由正整数构成的数表,用
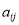 表示第
表示第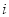 行第
行第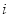 个数(
个数(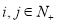 ). 此表中
). 此表中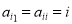 ,每行中除首尾两数外,其他各数分别等于其“肩膀”上的两数之和.
,每行中除首尾两数外,其他各数分别等于其“肩膀”上的两数之和.
(1)写出数表的第6行(从左至右依次列出);
(2)设第
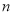 行的第二个数为
行的第二个数为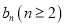 ,求
,求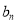 ;
;(3)令
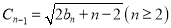 ,记
,记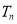 为数列
为数列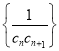 前
前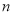 项和,求
项和,求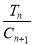 的最大值,并求此时
的最大值,并求此时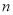 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人独立地对某一技术难题进行攻关.甲能攻克的概率为
 ,乙能攻克的概率为
,乙能攻克的概率为  ,丙能攻克的概率为
,丙能攻克的概率为  .
.
(1)求这一技术难题被攻克的概率;
(2)若该技术难题末被攻克,上级不做任何奖励;若该技术难题被攻克,上级会奖励a万元.奖励规则如下:若只有1人攻克,则此人获得全部奖金a万元;若只有2人攻克,则奖金奖给此二人,每人各得 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得  万元.设甲得到的奖金数为X,求X的分布列和数学期望.
万元.设甲得到的奖金数为X,求X的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn , 且a1=2,an+1=2Sn+2.
(1)求数列{an}的通项公式;
(2)若数列{bn}的各项均为正数,且bn是 与
与  的等比中项,求bn的前n项和Tn .
的等比中项,求bn的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】在
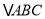 中,角
中,角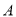 、
、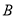 、
、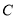 的对边分别为
的对边分别为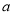 、
、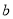 、
、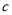 ,向量
,向量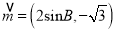 ,
,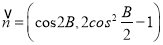 ,且
,且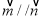 .
.(1)求锐角B的大小;
(2)在(1)的条件下,如果b=2,求
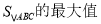 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=.
 ,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
A.
B.
C.
D.
相关试题

