【题目】已知f(x)=a(x﹣lnx)+ ![]() ,a∈R.
,a∈R.
(1)讨论f(x)的单调性;
(2)当a=1时,证明f(x)>f′(x)+ ![]() 对于任意的x∈[1,2]成立.
对于任意的x∈[1,2]成立.
参考答案:
【答案】
(1)
解:由f(x)=a(x﹣lnx)+ ![]() ,
,
得f′(x)=a(1﹣ ![]() )+
)+ ![]()
= ![]() =
= ![]() =
= ![]() (x>0).
(x>0).
若a≤0,则ax2﹣2<0恒成立,
∴当x∈(0,1)时,f′(x)>0,f(x)为增函数,
当x∈(1,+∞)时,f′(x)<0,f(x)为减函数;
当a>0,若0<a<2,当x∈(0,1)和( ![]() ,+∞)时,f′(x)>0,f(x)为增函数,
,+∞)时,f′(x)>0,f(x)为增函数,
当x∈(1, ![]() )时,f′(x)<0,f(x)为减函数;
)时,f′(x)<0,f(x)为减函数;
若a=2,f′(x)≥0恒成立,f(x)在(0,+∞)上为增函数;
若a>2,当x∈(0, ![]() )和(1,+∞)时,f′(x)>0,f(x)为增函数,
)和(1,+∞)时,f′(x)>0,f(x)为增函数,
当x∈( ![]() ,1)时,f′(x)<0,f(x)为减函数
,1)时,f′(x)<0,f(x)为减函数
(2)
解:∵a=1,
令F(x)=f(x)﹣f′(x)=x﹣lnx ![]() ﹣1
﹣1 ![]() =x﹣lnx+
=x﹣lnx+ ![]() .
.
∵ex>1+x,
∴x>ln(1+x),
∴ex﹣1>x,则x﹣1>lnx,
∴F(x)> ![]() =
= ![]() .
.
令φ(x)= ![]() ,则φ′(x)=
,则φ′(x)= ![]() =
= ![]() (x∈[1,2]).
(x∈[1,2]).
∴φ(x)在[1,2]上为减函数,则φ(x)![]() ,
,
∴F(x)> ![]() 恒成立.
恒成立.
即f(x)>f′(x)+ ![]() 对于任意的x∈[1,2]成立
对于任意的x∈[1,2]成立
【解析】(1)求出原函数的导函数,然后对a分类分析导函数的符号,由导函数的符号确定原函数的单调性;
(2)构造函数F(x)=f(x)﹣f′(x),求导后利用不等式x﹣1>lnx放缩,得到F(x)> ![]() =
= ![]() .令φ(x)=
.令φ(x)= ![]() ,利用导数可得φ(x)在[1,2]上为减函数,得到F(x)>
,利用导数可得φ(x)在[1,2]上为减函数,得到F(x)> ![]() 恒成立.由此可得f(x)>f′(x)+
恒成立.由此可得f(x)>f′(x)+ ![]() 对于任意的x∈[1,2]成立.
对于任意的x∈[1,2]成立.
本题考查利用导数加以函数的单调性,考查了利用导数求函数的最值,考查了分类讨论的数学思想方法和数学转化思想方法,是压轴题.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一个人猜对,则“星队”得1分;如果两人都没猜对,则“星队”得0分.已知甲每轮猜对的概率是
 ,乙每轮猜对的概率是
,乙每轮猜对的概率是  ;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
(1)“星队”至少猜对3个成语的概率;
(2)“星队”两轮得分之和为X的分布列和数学期望EX. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
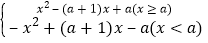 .
.(1)若f(2)=a,求a的值;
(2)当a=2时,若对任意互不相等的实数x1,x2∈(m,m+4),都有
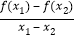 >0成立,求实数m的取值范围;
>0成立,求实数m的取值范围;(3)判断函数g(x)=f(x)-x-2a(
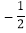 <a<0)在R上的零点的个数,并说明理由.
<a<0)在R上的零点的个数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】据某气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即时间t(h)内沙尘暴所经过的路程s(km).

(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,椭圆C:
 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是  ,抛物线E:x2=2y的焦点F是C的一个顶点.
,抛物线E:x2=2y的焦点F是C的一个顶点. 
(1)求椭圆C的方程;
(2)设P是E上的动点,且位于第一象限,E在点P处的切线l与C交与不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
①求证:点M在定直线上;
②直线l与y轴交于点G,记△PFG的面积为S1 , △PDM的面积为S2 , 求 的最大值及取得最大值时点P的坐标.
的最大值及取得最大值时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)判断f(x)的奇偶性,说明理由;
(2)当x>0时,判断f(x)的单调性并加以证明;
(3)若f(2t)-mf(t)>0对于t∈(0,+∞)恒成立,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是______(填上所有符合条件的序号)
①y=e-x在R上为增函数
②任取x>0,均有3x>2x
③函数y=f(x)的图象与直线x=a可能有两个交点
④y=2|x|的最小值为1;
⑤与y=3x的图象关于直线y=x对称的函数为y=log3x.
相关试题

