【题目】已知函数f(x)=![]() .
.
(1)若f(2)=a,求a的值;
(2)当a=2时,若对任意互不相等的实数x1,x2∈(m,m+4),都有![]() >0成立,求实数m的取值范围;
>0成立,求实数m的取值范围;
(3)判断函数g(x)=f(x)-x-2a(![]() <a<0)在R上的零点的个数,并说明理由.
<a<0)在R上的零点的个数,并说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 个零点,理由见解析.
个零点,理由见解析.
【解析】
(1)分类讨论求出f(2),代入 f(2)=a,解方程可得;
(2)a=2时,求出分段函数的增区间;“对任意互不相等的实数x1,x2∈(m,m+4),都有![]() 0成立”f(x)在(m,m+4)上是增函数,根据子集关系列式可得m的范围;
0成立”f(x)在(m,m+4)上是增函数,根据子集关系列式可得m的范围;
(3)按照x≥a和x<a这2种情况分别讨论零点个数.
解:(1)因为f(2)=a,
当a≤2时,4-2(a+1)+a=a,解得a=1符合;
当a<2时,-4+2(a+1)-a=a,此式无解;
综上可得:a=1.
(2)当a=2时,f(x)=![]() ,
,
∴f(x)的单调增区间为(-∞,![]() )和(2,+∞),
)和(2,+∞),
又由已知可得f(x)在(m,m+4)上单调递增,
所以m+4≤![]() ,或m≥2,
,或m≥2,
解得m≤-![]() 或m≥2,
或m≥2,
∴实数m的取值范围是(-∞,-![]() ]∪[2,+∞);
]∪[2,+∞);
(3)由题意得g(x)=![]()
①当x≥a时,对称轴为x=![]() ,
,
因为-![]() ,
,
所以f(a)=a2-a2-2a-a=-3a>0,
∵![]() -a=
-a=![]() >a,
>a,
∴f(![]() )=-
)=-![]() =-
=-![]() <0,
<0,
由二次函数可知,g(x)在区间(a,![]() )和区间(
)和区间(![]() ,+∞)各有一个零点;
,+∞)各有一个零点;
②当x<a时,对称轴为x=![]() >a,
>a,
函数g(x)在区间(-∞,a)上单调递增且f(![]() )=0,
)=0,
所以函数在区间(-∞,a)内有一个零点.
综上函数g(x)=f(x)-x-2a(-![]() <a<0)在R上有3个零点.
<a<0)在R上有3个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.
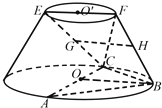
(1)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(2)已知EF=FB= AC=2
AC=2 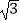 AB=BC,求二面角F﹣BC﹣A的余弦值.
AB=BC,求二面角F﹣BC﹣A的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1 .
(1)求数列{bn}的通项公式;
(2)令cn=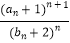 ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一个人猜对,则“星队”得1分;如果两人都没猜对,则“星队”得0分.已知甲每轮猜对的概率是
 ,乙每轮猜对的概率是
,乙每轮猜对的概率是  ;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
(1)“星队”至少猜对3个成语的概率;
(2)“星队”两轮得分之和为X的分布列和数学期望EX. -
科目: 来源: 题型:
查看答案和解析>>【题目】据某气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即时间t(h)内沙尘暴所经过的路程s(km).

(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=a(x﹣lnx)+
 ,a∈R.
,a∈R.
(1)讨论f(x)的单调性;
(2)当a=1时,证明f(x)>f′(x)+ 对于任意的x∈[1,2]成立.
对于任意的x∈[1,2]成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,椭圆C:
 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是  ,抛物线E:x2=2y的焦点F是C的一个顶点.
,抛物线E:x2=2y的焦点F是C的一个顶点. 
(1)求椭圆C的方程;
(2)设P是E上的动点,且位于第一象限,E在点P处的切线l与C交与不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
①求证:点M在定直线上;
②直线l与y轴交于点G,记△PFG的面积为S1 , △PDM的面积为S2 , 求 的最大值及取得最大值时点P的坐标.
的最大值及取得最大值时点P的坐标.
相关试题

