【题目】设函数f(x)=|x+m|.
(Ⅰ) 解关于m的不等式f(1)+f(﹣2)≥5;
(Ⅱ)当x≠0时,证明: ![]() .
.
参考答案:
【答案】解:(Ⅰ)不等式f(1)+f(﹣2)≥5等价于|m+1|+|m﹣2|≥5,
可化为 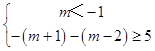 ,解得m≤﹣2;
,解得m≤﹣2;
或  ,无解;
,无解;
或  ,解得m≥3;
,解得m≥3;
综上不等式解集为(﹣∞,﹣2]∪[3,+∞)
(Ⅱ)证明:当x≠0时, ![]() ,|x|>0,
,|x|>0,![]()
【解析】(Ⅰ)问题等价于|m+1|+|m﹣2|≥5,通过讨论m的范围,求出不等式的解集即可;(Ⅱ)根据绝对值的性质证明即可.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正整数数列
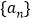 满足
满足 ,对于给定的正整数
,对于给定的正整数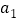 ,若数列
,若数列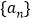 中首个值为1的项为
中首个值为1的项为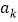 ,我们定义
,我们定义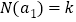 ,则
,则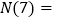 _____.设集合
_____.设集合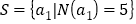 ,则集合
,则集合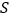 中所有元素的和为_____.
中所有元素的和为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4﹣4:极坐标与参数方程
极坐标系与直角坐标系xOy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知曲线C1的极坐标方程为 ,曲线C2的极坐标方程为ρsinθ=a(a>0),射线
,曲线C2的极坐标方程为ρsinθ=a(a>0),射线  ,
,  与曲线C1分别交异于极点O的四点A,B,C,D.
与曲线C1分别交异于极点O的四点A,B,C,D.
(Ⅰ)若曲线C1关于曲线C2对称,求a的值,并把曲线C1和C2化成直角坐标方程;
(Ⅱ)求|OA||OC|+|OB||OD|的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 菱形
菱形 所在平面,
所在平面, ,
, 为线段
为线段 的中点,
的中点,  为线段
为线段 上一点,且
上一点,且 .
.
(1)求证:
 平面
平面 ;
;(2)若
 ,求二面角
,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设向量
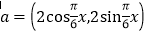 ,
, ,令函数
,令函数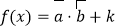 ,若函数
,若函数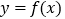 的部分图象如图所示,且点
的部分图象如图所示,且点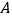 的坐标为
的坐标为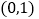 .
.
(1)求点
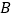 的坐标;
的坐标;(2)求函数
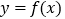 的单调增区间及对称轴方程;
的单调增区间及对称轴方程;(3)若把方程
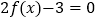 的正实根从小到大依次排列为
的正实根从小到大依次排列为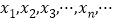 ,求
,求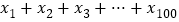 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
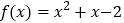 ,
,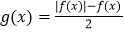
(1)写出函数
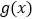 的解析式;
的解析式;(2)若直线
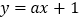 与曲线
与曲线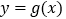 有三个不同的交点,求
有三个不同的交点,求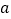 的取值范围;
的取值范围;(3)若直线
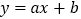 与曲线
与曲线 在
在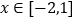 内有交点,求
内有交点,求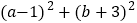 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.(1)求椭圆
 的方程;
的方程;(2)设点
 是轨迹
是轨迹 上位于第一象限且在直线
上位于第一象限且在直线 右侧的动点,若以
右侧的动点,若以 为圆心,线段
为圆心,线段 为半径的圆
为半径的圆 与
与 有两个公共点.试求圆
有两个公共点.试求圆 在右焦点
在右焦点 处的切线
处的切线 与
与 轴交点纵坐标的取值范围.
轴交点纵坐标的取值范围.
相关试题

