【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是轨迹
是轨迹![]() 上位于第一象限且在直线
上位于第一象限且在直线![]() 右侧的动点,若以
右侧的动点,若以![]() 为圆心,线段
为圆心,线段![]() 为半径的圆
为半径的圆![]() 与
与![]() 有两个公共点.试求圆
有两个公共点.试求圆![]() 在右焦点
在右焦点![]() 处的切线
处的切线![]() 与
与![]() 轴交点纵坐标的取值范围.
轴交点纵坐标的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)由题知,原点到直线![]() 的距离,求得
的距离,求得![]() ,再由
,再由![]() ,求得
,求得![]() ,即可得到椭圆的标准方程;
,即可得到椭圆的标准方程;
(2)设![]() ,由圆的方程和性质
,由圆的方程和性质![]() ,又由椭圆的方程得
,又由椭圆的方程得![]() ,代入可得
,代入可得![]() ,求得
,求得![]() ,又由切线
,又由切线![]() 方程为
方程为![]() ,令
,令![]() 得
得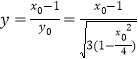 ,令
,令![]() ,利用二次函数的性质,即可求解得
,利用二次函数的性质,即可求解得![]() 的范围,即可得到结论.
的范围,即可得到结论.
详解:(1)由题知,原点到直线![]() 的距离
的距离
![]()
![]()
又![]() ,则
,则![]()
![]()
∴椭圆![]() 方程为
方程为
![]() ………………4分
………………4分
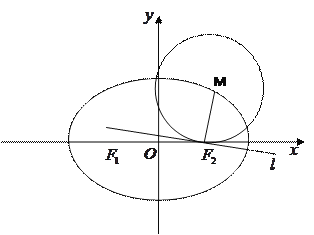
(2)设![]() ,点
,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,
,
![]()
∵圆M与y轴有两个交点,∴![]() ,
,
即![]() ,
,
∴![]() ,
,
又![]() ,
,
即![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() , ……………………7分
, ……………………7分
又![]() ,∴
,∴![]() ……………………8分
……………………8分
切线![]() 方程为
方程为![]() ,令
,令![]() 得
得
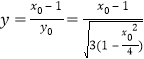
令![]() ,则
,则![]()
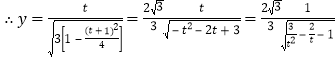 ……………10分
……………10分
![]() ,则
,则![]() ,
,![]() 在
在![]()
∴![]()
![]()
∴切线![]() 与
与![]() 轴交点纵坐标的取值范围为
轴交点纵坐标的取值范围为![]() ……………………12分
……………………12分
(转化为求![]() 的斜率范围得到更为简便)
的斜率范围得到更为简便)
解法2:上面步骤相同
又![]() ,∴
,∴![]() ……………………8分
……………………8分
切线![]() 方程为
方程为![]() ,令
,令![]() 得
得![]()
又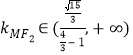 即
即![]()
![]()
∴切线![]() 与
与![]() 轴交点纵坐标的取值范围为
轴交点纵坐标的取值范围为![]() ……………………12分
……………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|x+m|.
(Ⅰ) 解关于m的不等式f(1)+f(﹣2)≥5;
(Ⅱ)当x≠0时,证明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设向量
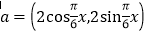 ,
, ,令函数
,令函数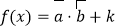 ,若函数
,若函数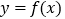 的部分图象如图所示,且点
的部分图象如图所示,且点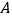 的坐标为
的坐标为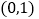 .
.
(1)求点
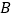 的坐标;
的坐标;(2)求函数
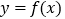 的单调增区间及对称轴方程;
的单调增区间及对称轴方程;(3)若把方程
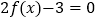 的正实根从小到大依次排列为
的正实根从小到大依次排列为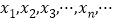 ,求
,求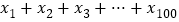 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
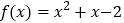 ,
,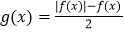
(1)写出函数
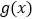 的解析式;
的解析式;(2)若直线
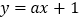 与曲线
与曲线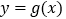 有三个不同的交点,求
有三个不同的交点,求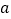 的取值范围;
的取值范围;(3)若直线
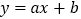 与曲线
与曲线 在
在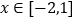 内有交点,求
内有交点,求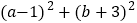 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在2018年高校自主招生期间,某校把学生的平时成绩按“百分制”折算,选出前
 名学生,并对这
名学生,并对这 名学生按成绩分组,第一组
名学生按成绩分组,第一组 ,第二组
,第二组 ,第三组
,第三组 ,第四组
,第四组 ,第五组
,第五组 .如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
.如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
(1)请写出第一、二、三、五组的人数,并在图中补全频率分布直方图;
(2)若
 大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试.
大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试.①若
 大学本次面试中有
大学本次面试中有 ,
, ,
,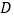 三位考官,规定获得至少两位考官的认可即为面试成功,且各考官面试结果相互独立.已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为
三位考官,规定获得至少两位考官的认可即为面试成功,且各考官面试结果相互独立.已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为 ,
, ,
, ,求甲同学面试成功的概率;
,求甲同学面试成功的概率;②若
 大学决定在这6名学生中随机抽取3名学生接受考官
大学决定在这6名学生中随机抽取3名学生接受考官 的面试,第3组有
的面试,第3组有 名学生被考官
名学生被考官 面试,求
面试,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知海岛
 在海岛
在海岛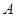 北偏东
北偏东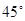 ,
,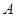 ,
, 相距
相距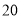 海里,物体甲从海岛
海里,物体甲从海岛 以
以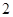 海里/小时的速度沿直线向海岛
海里/小时的速度沿直线向海岛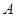 移动,同时物体乙从海岛
移动,同时物体乙从海岛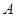 沿着海岛
沿着海岛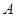 北偏西
北偏西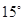 方向以
方向以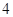 海里/小时的速度移动.
海里/小时的速度移动.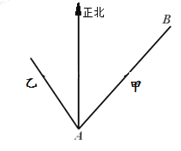
(1)问经过多长时间,物体甲在物体乙的正东方向;
(2)求甲从海岛
 到达海岛
到达海岛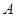 的过程中,甲、乙两物体的最短距离.
的过程中,甲、乙两物体的最短距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
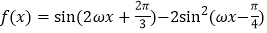 ,
, .
.(1)当
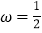 时,求函数
时,求函数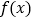 的单调递增区间;
的单调递增区间;(2)对于
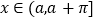 ,
,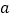 为任意实数,关于
为任意实数,关于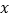 的方程
的方程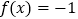 恰好有两个不等实根,求实数
恰好有两个不等实根,求实数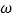 的值;
的值;(3)在(2)的条件下,若不等式
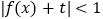 在
在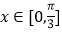 恒成立,求实数
恒成立,求实数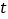 的取值范围.
的取值范围.
相关试题

