【题目】若由方程x2-y2=0和x2+(y-b)2=2所组成的方程组至多有两组不同的实数解,则实数b的取值范围是( )
A. b≥2![]() 或b≤-2
或b≤-2![]() B. b≥2或b≤-2
B. b≥2或b≤-2
C. -2≤b≤2 D. -2![]() ≤b≤2
≤b≤2![]()
参考答案:
【答案】B
【解析】
方程x2-y2=0和x2+(y-b)2=2所组成的方程组至多有两组不同的实数解可转化为,当圆x2+(y-b)2=2与两条直线![]() 都相切时,即
都相切时,即![]() 或
或![]() 时,圆与直线有两个交点,当圆与直线相离时无交点,此时
时,圆与直线有两个交点,当圆与直线相离时无交点,此时![]() 或
或![]() ,即可得出结论.
,即可得出结论.
因为方程x2-y2=0和x2+(y-b)2=2分别表示直线和圆
所以方程x2-y2=0和x2+(y-b)2=2所组成的方程组至多有两组不同的实数解可转化为直线与圆至多有两个交点,当圆x2+(y-b)2=2与两条直线![]() 都相切时,根据圆心到直线的距离等半径可得
都相切时,根据圆心到直线的距离等半径可得![]() ,即
,即![]() 或
或![]() 时,圆与直线有两个交点,当圆与直线相离时无交点,此时
时,圆与直线有两个交点,当圆与直线相离时无交点,此时![]() 或
或![]() ,综上可知 b≥2或b≤-2,
,综上可知 b≥2或b≤-2,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
袋中有形状和大小完全相同的四种不同颜色的小球,每种颜色的小球各有4个,分别编号为1,2,3,4.现从袋中随机取两个球.
(Ⅰ)若两个球颜色不同,求不同取法的种数;
(Ⅱ)在(1)的条件下,记两球编号的差的绝对值为随机变量X,求随机变量X的概率分布与数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为调查某社区年轻人的周末生活状况,研究这一社区年轻人在周末的休闲方式与性别的关系,随机调查了该社区年轻人80人,得到下面的数据表:

(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的年轻男性,设调查的3人在这一时间段以上网为休闲方式的人数为随机变量X,求X的分布列和数学期望;
(2)根据以上数据,能否有99%的把握认为“周末年轻人的休闲方式与性别有关系”?
参考公式:

参考数据:

0.05
0.010

3.841
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】知函数
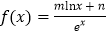 (
(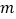 、
、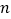 为常数),曲线
为常数),曲线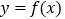 在点
在点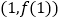 处的切线方程是
处的切线方程是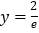 .
.(1)求
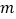 、
、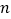 的值
的值 (2)求
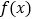 的最大值
的最大值(3)设
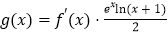 ,证明:对任意
,证明:对任意 ,都有
,都有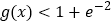 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”,《中华人民共和国道路交通安全法》 第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为统计数据:
月份
1
2
3
4
5
违章驾驶员人数
120
105
100
90
85
(1)请利用所给数据求违章人数y与月份之间的回归直线方程
 +
+
(2)预测该路口7月份的不“礼让斑马线”违章驾驶员人数;
(3)交警从这5个月内通过该路口的驾驶员中随机抽查了50人,调查驾驶员不“礼让斑马线”行为与驾龄的关系,得到如下2
 列联表:
列联表:不礼让斑马线
礼让斑马线
合计
驾龄不超过1年
22
8
30
驾龄1年以上
8
12
20
合计
30
20
50
能否据此判断有97.5
 的把握认为“礼让斑马线”行为与驾龄有关?
的把握认为“礼让斑马线”行为与驾龄有关?参考公式及数据:
 ,
, .
.
0.150
0.100
0.050
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
 (其中n=a+b+c+d)
(其中n=a+b+c+d) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆 C:
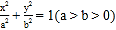 的焦距为2,且过点
的焦距为2,且过点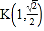 ,右焦点为
,右焦点为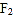 .设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为
.设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为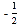 ,线段AB的中垂线交椭圆C于P,Q 两点.
,线段AB的中垂线交椭圆C于P,Q 两点.
(1)求椭圆 C 的方程;
(2)设M点纵坐标为m,求直线PQ的方程,并求
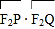 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
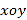 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为1, 圆心在
的半径为1, 圆心在 上.
上.
(1)若圆心
 也在直线
也在直线 上,过点
上,过点 作圆
作圆 的切线,求切线方程;
的切线,求切线方程;(2)若圆
 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围.
相关试题

