【题目】等差数列{an}中,其前n项和为Sn , 且 ![]() ,等比数列{bn}中,其前n项和为Tn , 且
,等比数列{bn}中,其前n项和为Tn , 且 ![]() ,(n∈N*)
,(n∈N*)
(1)求an , bn;
(2)求{anbn}的前n项和Mn .
参考答案:
【答案】
(1)解:法1:由 ![]() ,a1=1
,a1=1
又 ![]() ,所以a2=3或﹣1
,所以a2=3或﹣1
因为a2=﹣1时, ![]() =1,故a2=﹣1舍去
=1,故a2=﹣1舍去
所以等差数列{an)的公差d=a2﹣a1=2∴an=2n﹣1,
同样可得b1=1,b2=3或﹣1
因为b2=3时, ![]() ,故b2=3舍去
,故b2=3舍去
又{bn}为等比数列,所以 ![]()
法2: ![]() ,a1=1…1分
,a1=1…1分 ![]() ,
, ![]() ,(n≥2)
,(n≥2) 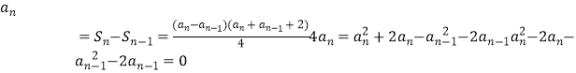 (an﹣an﹣1)(an+an﹣1)﹣2(an+an﹣1)=0
(an﹣an﹣1)(an+an﹣1)﹣2(an+an﹣1)=0
(an﹣an﹣1﹣2)(an+an﹣1)=0,因为{an}为等差数列,
所以an﹣an﹣1﹣2=0,又a1=1∴an=2n﹣1,
又{bn}为等比数列,所以易得 ![]()
(2)解:法一:Mn=a1b1+a2b2+…+anbn=1﹣3+5﹣7+…+(﹣1)n﹣1(2n﹣1)
若n为偶数,则Mn= ![]()
所以Mn=﹣n
若n为奇数,则结合上边情况可得 Mn=﹣(n﹣1)+(2n﹣1)=n
综上可得Mn=(﹣1)n﹣1n
法二:Mn=1×(﹣1)0+3×(﹣1)1+5×(﹣1)2+…+(2n﹣1)×(﹣1)n﹣1…①
﹣Mn=1×(﹣1)1+3×(﹣1)2+5×(﹣1)3+…+(2n﹣1)×(﹣1)n…②
①﹣②得:
2Mn=1+2×(﹣1)1+2×(﹣1)2+2×(﹣1)3+…+2×(﹣1)n﹣1﹣(2n﹣1)×(﹣1)n
2Mn= ![]() Mn=n×(﹣1)n﹣1
Mn=n×(﹣1)n﹣1
【解析】(1)法1:利用等差数列的前3项求出公差与首项,再利用通项公式即可得出.法2:利用递推关系与等差数列的通项公式即可得出.(2)法1:利用分组求和即可得出.法2:利用“错位相减法”与等比数列的求和公式即可得出.
【考点精析】根据题目的已知条件,利用等差数列的通项公式(及其变式)和数列的前n项和的相关知识可以得到问题的答案,需要掌握通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正三角形
 的边长为
的边长为 ,将它沿高
,将它沿高 翻折,使点
翻折,使点 与点
与点 间的距离为
间的距离为 ,此时四面体
,此时四面体 外接球表面积为
外接球表面积为A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)满足
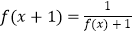 ,当x∈[0,1]时,f(x)=x,若在区间(﹣1,1]上,方程f(x)﹣4ax﹣a=0有两个不等的实根,则实数a的取值范围是 .
,当x∈[0,1]时,f(x)=x,若在区间(﹣1,1]上,方程f(x)﹣4ax﹣a=0有两个不等的实根,则实数a的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费用支出
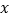 与销售额
与销售额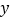 之间有如下的对应数据(单位:万元):
之间有如下的对应数据(单位:万元):
(1)求
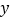 关于
关于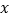 的线性回归直线方程;
的线性回归直线方程;(2)据此估计广告费用为10万元时销售收入
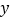 的值.
的值.(附:对于线性回归方程
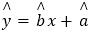 ,其中
,其中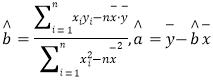 )
)参考公式:
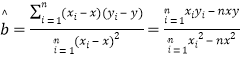
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如表:
消费次第
第1次
第2次
第3次
第4次
≥5次
收费比例
1
0.95
0.90
0.85
0.80
该公司从注册的会员中,随机抽取了100位进行统计,得到统计数据如表:
消费次第
第1次
第2次
第3次
第4次
第5次
频数
60
20
10
5
5
假设汽车美容一次,公司成本为150元,根据所给数据,解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(3)设该公司从至少消费两次,求这的顾客消费次数用分层抽样方法抽出8人,再从这8人中抽出2人发放纪念品,求抽出2人中恰有1人消费两次的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE=
 .
. 
(1)求证:AB⊥平面BCF;
(2)求直线AE与平面BDE所成角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(﹣3,0),点P在y轴上,点Q在x轴的正半轴上,点N在直线PQ上,且满足
 . (Ⅰ)当点P在y轴上移动时,求点N的轨迹C的方程;
. (Ⅰ)当点P在y轴上移动时,求点N的轨迹C的方程;
(Ⅱ)过点 做直线l与轨迹C交于A,B两点,若在x轴上存在一点E(x0 , 0),使得△AEB是以点E为直角顶点的直角三角形,求直线l的斜率k的取值范围.
做直线l与轨迹C交于A,B两点,若在x轴上存在一点E(x0 , 0),使得△AEB是以点E为直角顶点的直角三角形,求直线l的斜率k的取值范围.
相关试题

