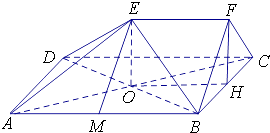
【题目】如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE= ![]() .
. 
(1)求证:AB⊥平面BCF;
(2)求直线AE与平面BDE所成角的正切值.
参考答案:
【答案】
(1)证明:取AB的中点M,连接EM,则AM=MB=1,
∵EF∥平面ABCD,EF平面ABEF,平面ABCD∩平面ABEF=AB,
∴EF∥AB,即EF∥MB.
∵EF=MB=1
∴四边形EMBF是平行四边形.
∴EM∥FB,EM=FB.
在Rt△BFC中,FB2+FC2=BC2=4,又FB=FC,得FB= ![]() .
.
∴EM= ![]() .
.
在△AEM中,AE= ![]() ,AM=1,EM=
,AM=1,EM= ![]() ,
,
∴AM2+EM2=3=AE2,
∴AM⊥EM.
∴AM⊥FB,即AB⊥FB.
∵四边形ABCD是正方形,
∴AB⊥BC.
∵FB∩BC=B,FB平面BCF,BC平面BCF,
∴AB⊥平面BCF.
(2)解:连接AC,AC与BD相交于点O,则点O是AC的中点,
取BC的中点H,连接OH,EO,FH,
则OH∥AB,OH= ![]() AB=1.
AB=1.
由(1)知EF∥AB,且EF= ![]() AB,
AB,
∴EF∥OH,且EF=OH.
∴四边形EOHF是平行四边形.
∴E0∥FH,且EO=FH=1.
由(1)知AB⊥平面BCF,又FH平面BCF,
∴FH⊥AB,
∵FH⊥BC,AB∩BC=B,FH平面ABCD,BC平面ABCD,
∴FH⊥平面ABCD.
∴E0⊥平面ABCD.
∵AO平面ABCD,
∴EO⊥AO.
∵AO⊥BD,EO∩BD=O,EO平面EBD,BD平面EBD,
∴AO⊥平面EBD.
∴∠AEO是直线AE与平面BDE所成的角.
在Rt△AOE中,tan∠AEO= ![]() =
= ![]() .
.
∴直线AE与平面BDE所成角的正切值为 ![]() .
.
【解析】(1)先证明出四边形EMBF是平行四边形,推断出EM∥FB,EM=FB.进而在Rt△BFC中求得EM,在△AEM中,根据边长推断出AM2+EM2=3=AE2 , 进而证明出AM⊥EM.然后证明出四边形ABCD是正方形,进而推断出AB⊥BC.最后通过线面垂直的判定定理证明出AB⊥平面BCF.(2)先证明出∠AEO是直线AE与平面BDE所成的角,进而在Rt△AOE中,求得tan∠AEO.
【考点精析】通过灵活运用直线与平面垂直的判定和空间角的异面直线所成的角,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则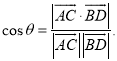 即可以解答此题.
即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费用支出
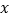 与销售额
与销售额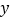 之间有如下的对应数据(单位:万元):
之间有如下的对应数据(单位:万元):
(1)求
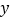 关于
关于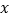 的线性回归直线方程;
的线性回归直线方程;(2)据此估计广告费用为10万元时销售收入
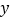 的值.
的值.(附:对于线性回归方程
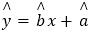 ,其中
,其中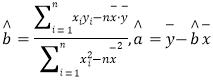 )
)参考公式:
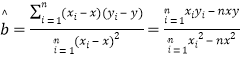
-
科目: 来源: 题型:
查看答案和解析>>【题目】等差数列{an}中,其前n项和为Sn , 且
 ,等比数列{bn}中,其前n项和为Tn , 且
,等比数列{bn}中,其前n项和为Tn , 且  ,(n∈N*)
,(n∈N*)
(1)求an , bn;
(2)求{anbn}的前n项和Mn . -
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如表:
消费次第
第1次
第2次
第3次
第4次
≥5次
收费比例
1
0.95
0.90
0.85
0.80
该公司从注册的会员中,随机抽取了100位进行统计,得到统计数据如表:
消费次第
第1次
第2次
第3次
第4次
第5次
频数
60
20
10
5
5
假设汽车美容一次,公司成本为150元,根据所给数据,解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(3)设该公司从至少消费两次,求这的顾客消费次数用分层抽样方法抽出8人,再从这8人中抽出2人发放纪念品,求抽出2人中恰有1人消费两次的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(﹣3,0),点P在y轴上,点Q在x轴的正半轴上,点N在直线PQ上,且满足
 . (Ⅰ)当点P在y轴上移动时,求点N的轨迹C的方程;
. (Ⅰ)当点P在y轴上移动时,求点N的轨迹C的方程;
(Ⅱ)过点 做直线l与轨迹C交于A,B两点,若在x轴上存在一点E(x0 , 0),使得△AEB是以点E为直角顶点的直角三角形,求直线l的斜率k的取值范围.
做直线l与轨迹C交于A,B两点,若在x轴上存在一点E(x0 , 0),使得△AEB是以点E为直角顶点的直角三角形,求直线l的斜率k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+x﹣lnx,(a>0). (Ⅰ)求f(x)的单调区间;
(Ⅱ)设f(x)极值点为x0 , 若存在x1 , x2∈(0,+∞),且x1≠x2 , 使f(x1)=f(x2),求证:x1+x2>2x0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 与坐标轴的交点都在圆
与坐标轴的交点都在圆 上.
上.(1)求圆
 的方程;
的方程;(2)若圆
 与直线
与直线 交于
交于 ,
, 两点,且
两点,且 ,求
,求 的值.
的值.
相关试题

