【题目】已知椭圆![]() :
: ![]() ,
, ![]() 分别是其左、右焦点,以线段
分别是其左、右焦点,以线段![]() 为直径的圆与椭圆
为直径的圆与椭圆![]() 有且仅有两个交点.
有且仅有两个交点.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线![]() 交椭圆于
交椭圆于![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,点
,点![]() 横坐标的取值范围是
横坐标的取值范围是![]() ,求
,求![]() 的最小值.
的最小值.
参考答案:
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(1)由椭圆几何条件可得![]() ,因此
,因此![]() ,(2) 将直线
,(2) 将直线![]() 方程与椭圆方程联立,结合韦达定理以及弦长公式可得
方程与椭圆方程联立,结合韦达定理以及弦长公式可得![]() 关于直线
关于直线![]() 斜率的函数关系式,再根据中点坐标公式列出线段
斜率的函数关系式,再根据中点坐标公式列出线段![]() 的垂直平分线,并求与
的垂直平分线,并求与![]() 轴交点
轴交点![]() 横坐标,根据点
横坐标,根据点![]() 横坐标的取值范围,确定直线
横坐标的取值范围,确定直线![]() 斜率取值范围,最后根据直线
斜率取值范围,最后根据直线![]() 斜率取值范围确定
斜率取值范围确定![]() 的最小值.
的最小值.
试题解析:(Ⅰ) 由题意可知![]() ,
,
∴![]() ,故椭圆的方程为
,故椭圆的方程为![]() .
.
(Ⅱ) 设直线![]() 方程为
方程为![]() ,
,
代入![]() 有
有![]() ,
,
设![]() ,
, ![]() 中点
中点![]() ,
,
∴![]() .
.
∴![]()
∴![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,
,
令![]() ,得
,得![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
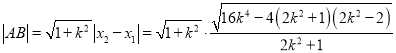
 ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
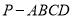 中,底面
中,底面 为正方形,
为正方形,  底面
底面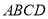 ,
, 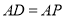 ,
, 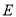 为棱
为棱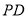 中点.
中点.
(1)求证:
 平面
平面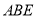 ;
;(2)若
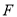 为
为 中点,
中点, 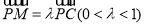 ,试确定
,试确定 的值,使二面角
的值,使二面角 的余弦值为
的余弦值为 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中错误的是( )
A. 如果平面
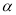 外的直线
外的直线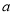 不平行于平面
不平行于平面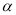 ,则平面
,则平面 内不存在与
内不存在与 平行的直线
平行的直线B. 如果平面
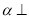 平面
平面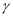 ,平面
,平面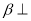 平面
平面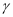 ,
, 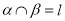 ,那么直线
,那么直线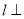 平面
平面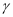
C. 如果平面
 平面
平面 ,那么平面
,那么平面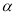 内所有直线都垂直于平面
内所有直线都垂直于平面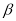
D. 一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交
-
科目: 来源: 题型:
查看答案和解析>>【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:

(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取2名用户,求2名用户评分小于90分的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
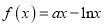 .
.(1)过原点
 作函数
作函数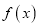 图象的切线,求切点的横坐标;
图象的切线,求切点的横坐标;(2)对
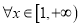 ,不等式
,不等式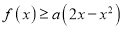 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求经过两直线2x-3y-3=0和x+y+2=0的交点且与直线3x+y-1=0平行的直线l的方程;
(2)求经过两直线l1:x-2y+4=0和l2:x+y-2=0的交点P,且与直线l3:3x-4y+5=0垂直的直线l的方程.
相关试题

