【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 中点.
中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 中点,
中点, ![]() ,试确定
,试确定![]() 的值,使二面角
的值,使二面角![]() 的余弦值为
的余弦值为![]() .
.
参考答案:
【答案】(I) 见解析; (II) ![]() .
.
【解析】试题分析:(1)证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的寻找与论证,往往从两个方面进行,一是利用条件中的线面垂直性质定理得到线线垂直,二是利用平几知识,如等腰三角形性质得到线线垂直,(2)研究二面角的大小,一般方法为利用空间向量数量积,即先根据条件建立恰当的空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,利用向量数量积求出两法向量夹角,再根据二面角与两法向量夹角关系列方程,解出参数.
试题解析:(I)证明:∵![]() 底面
底面![]() ,
, ![]() 底面
底面![]() ,∴
,∴![]() ,
,
又∵底面![]() 为矩形,∴
为矩形,∴![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,∴
中点,∴![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(II) 以![]() 为原点,以
为原点,以![]() 为
为![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系![]() ,令
,令![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
设平面![]() 的法向量
的法向量![]() ,
,  ,即
,即![]() ,
, ![]()
设平面![]() 的法向量
的法向量![]() ,
,  ,
,
即![]() ,
, ![]()
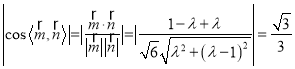 ,解得
,解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
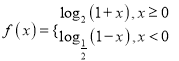 .
.(1)判断函数
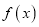 的奇偶性;
的奇偶性;(2)对任意两个实数
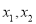 ,求证:当
,求证:当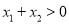 时,
时, 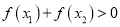 ;
;(3)对任何实数
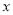 ,
, 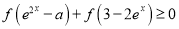 恒成立,求实数
恒成立,求实数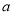 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,底面ABCD中,AB⊥AD,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
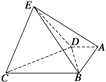
(1)求证:平面DEC⊥平面BDE;
(2)求点A到平面BDE的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中错误的是( )
A. 如果平面
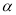 外的直线
外的直线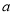 不平行于平面
不平行于平面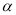 ,则平面
,则平面 内不存在与
内不存在与 平行的直线
平行的直线B. 如果平面
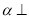 平面
平面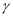 ,平面
,平面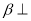 平面
平面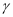 ,
, 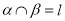 ,那么直线
,那么直线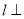 平面
平面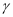
C. 如果平面
 平面
平面 ,那么平面
,那么平面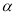 内所有直线都垂直于平面
内所有直线都垂直于平面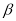
D. 一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
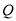 :
: 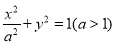 ,
, 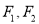 分别是其左、右焦点,以线段
分别是其左、右焦点,以线段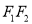 为直径的圆与椭圆
为直径的圆与椭圆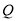 有且仅有两个交点.
有且仅有两个交点.(1)求椭圆
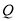 的方程;
的方程;(2)设过点
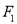 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线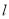 交椭圆于
交椭圆于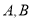 两点,线段
两点,线段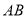 的垂直平分线与
的垂直平分线与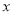 轴交于点
轴交于点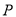 ,点
,点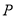 横坐标的取值范围是
横坐标的取值范围是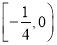 ,求
,求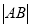 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:

(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取2名用户,求2名用户评分小于90分的概率.

相关试题

