【题目】已知函数![]() .
.
(1)过原点![]() 作函数
作函数![]() 图象的切线,求切点的横坐标;
图象的切线,求切点的横坐标;
(2)对![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(1)设切点坐标,利用导数几何意义以及切点在切线上,也在曲线上列方程组,解得切点的横坐标;(2)不等式恒成立问题往往转化为对应函数最值问题: ![]() 对
对![]() ,
, ![]() 恒成立等价于
恒成立等价于![]() 的最小值不小于零,根据导函数符号变化规律,分类讨论函数单调性,进而得函数最值,验证是否满足条件,确定实数
的最小值不小于零,根据导函数符号变化规律,分类讨论函数单调性,进而得函数最值,验证是否满足条件,确定实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)设切点为![]() ,直线的切线方程为
,直线的切线方程为![]()
, ![]() ,
,
即直线的切线方程为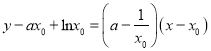
又切线过原点![]() ,所以
,所以![]() ,
,
由![]() ,解得
,解得![]() ,所以切点的横坐标为
,所以切点的横坐标为![]() .
.
(Ⅱ)方法一:∵不等式![]() 对
对![]() ,
, ![]() 恒成立,
恒成立,
∴![]() 对
对![]() ,
, ![]() 恒成立.
恒成立.
设![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() 在
在![]() ,
, ![]() 上单调递减,
上单调递减,
即![]() ,
, ![]() 不符合题意.
不符合题意.
②当![]() 时,
时, ![]() .设
.设![]() ,
,
在![]() ,
, ![]() 上单调递增,即
上单调递增,即![]() .
.
(ⅰ)当![]() 时,由
时,由![]() ,得
,得![]() ,
, ![]() 在
在![]() ,
, ![]() 上单调递增,即
上单调递增,即![]() ,
, ![]() 符合题意;
符合题意;
(ii)当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 使得
使得![]() ,
,
则![]() 在
在![]() ,
, ![]() 上单调递减,在
上单调递减,在![]() ,
, ![]() 上单调递增,
上单调递增,
![]() ,则
,则![]() 不合题意.
不合题意.
综上所述, ![]() .
.
(Ⅱ)方法二:∵不等式![]() 对
对![]() ,
, ![]() 恒成立,
恒成立,
∴![]() 对
对![]() ,
, ![]() 恒成立.
恒成立.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
![]() 不恒成立;同理
不恒成立;同理![]() 取其他值不恒成立.
取其他值不恒成立.
当![]() 时,
时, ![]() 恒成立;
恒成立;
当![]() 时,
时, ![]() ,证明
,证明![]() 恒成立.
恒成立.
设![]()
![]() ,
, ![]() ,
,
![]() .∴
.∴![]() 在
在![]() ,
, ![]() 为减函数.
为减函数.
![]() ,∴
,∴![]() .
.
(Ⅱ)方法三:∵不等式![]() 对
对![]() ,
,![]() 恒成立,
恒成立,
∴等价于![]() 对
对![]() ,
, ![]() 恒成立.
恒成立.
设![]() ,当
,当![]() 时,
时, ![]() ;∴
;∴![]() ,
,
函数![]() 过点(0,0)和(1,0),函数
过点(0,0)和(1,0),函数![]() 过点(1.0),
过点(1.0),![]() 在
在![]() 恒成立,
恒成立,
一定存在一条过点(1,0)的直线和函数![]() 、
、![]() 都相切或,一定存在一条过点(1,0)的直线
都相切或,一定存在一条过点(1,0)的直线![]() 相切和函数
相切和函数![]() 相交,但交点横坐标小于1,
相交,但交点横坐标小于1,
当都相切时![]() .
.
![]() 不大于等于0.
不大于等于0.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中错误的是( )
A. 如果平面
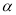 外的直线
外的直线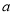 不平行于平面
不平行于平面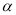 ,则平面
,则平面 内不存在与
内不存在与 平行的直线
平行的直线B. 如果平面
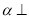 平面
平面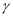 ,平面
,平面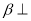 平面
平面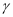 ,
, 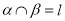 ,那么直线
,那么直线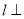 平面
平面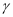
C. 如果平面
 平面
平面 ,那么平面
,那么平面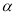 内所有直线都垂直于平面
内所有直线都垂直于平面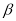
D. 一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
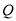 :
: 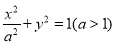 ,
, 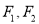 分别是其左、右焦点,以线段
分别是其左、右焦点,以线段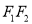 为直径的圆与椭圆
为直径的圆与椭圆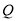 有且仅有两个交点.
有且仅有两个交点.(1)求椭圆
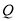 的方程;
的方程;(2)设过点
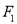 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线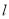 交椭圆于
交椭圆于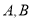 两点,线段
两点,线段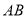 的垂直平分线与
的垂直平分线与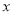 轴交于点
轴交于点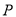 ,点
,点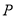 横坐标的取值范围是
横坐标的取值范围是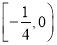 ,求
,求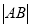 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:

(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取2名用户,求2名用户评分小于90分的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求经过两直线2x-3y-3=0和x+y+2=0的交点且与直线3x+y-1=0平行的直线l的方程;
(2)求经过两直线l1:x-2y+4=0和l2:x+y-2=0的交点P,且与直线l3:3x-4y+5=0垂直的直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
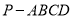 中,底面
中,底面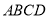 为正方形,
为正方形, 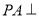 底面
底面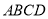 ,
, 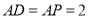 ,
, 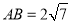 ,
, 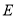 为棱
为棱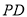 中点.
中点.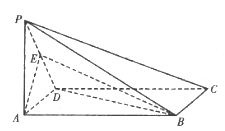
(1)求证:
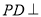 平面
平面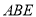 ;
;(2)求四棱锥
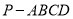 外接球的体积.
外接球的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】据某市地产数据研究的数据显示,2016年该市新建住宅销售均价走势如下图所示,为抑制房价过快上涨,政府从8月采取宏观调控措施,10月份开始房价得到很好的抑制.
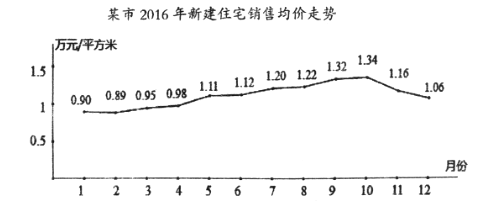
(1)地产数据研究院发现,3月至7月的各月均价
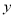 (万元/平方米)与月份
(万元/平方米)与月份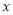 之间具有较强的线性相关关系,试建立
之间具有较强的线性相关关系,试建立 关于
关于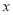 的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;(2)地产数据研究院在2016年的12个月份中,随机抽取三个月的数据作样本分析,若关注所抽三个月份的所属季度,记不同季度的个数为
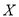 ,求
,求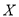 的分布列和数学期望.
的分布列和数学期望.参考数据:
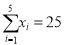 ,
, 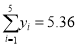 ,
, 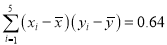 ;
;回归方程
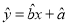 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: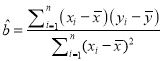 ,
, 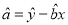 .
.
相关试题

