【题目】已知函数f(x)=|lgx|.若a≠b且,f(a)=f(b),则a+b的取值范围是( )
A.(1,+∞)
B.[1,+∞)
C.(2,+∞)
D.[2,+∞)
参考答案:
【答案】C
【解析】解:(方法一)因为f(a)=f(b),所以|lga|=|lgb|,
不妨设0<a<b,则0<a<1<b,∴lga=﹣lgb,lga+lgb=0
∴lg(ab)=0
∴ab=1,
又a>0,b>0,且a≠b
∴(a+b)2>4ab=4
∴a+b>2
故选:C.
(方法二)由对数的定义域,设0<a<b,且f(a)=f(b),得: 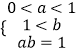 ,
,
整理得线性规划表达式为: 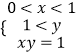 ,
,
因此问题转化为求z=x+y的取值范围问题,则z=x+yy=﹣x+z,即求函数的截距最值.
根据导数定义, ![]() 函数图象过点(1,1)时z有最小为2(因为是开区域,所以取不到2),
函数图象过点(1,1)时z有最小为2(因为是开区域,所以取不到2),
∴a+b的取值范围是(2,+∞).
故选:C.
【考点精析】认真审题,首先需要了解函数的值域(求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的),还要掌握对数函数的单调性与特殊点(过定点(1,0),即x=1时,y=0;a>1时在(0,+∞)上是增函数;0>a>1时在(0,+∞)上是减函数)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设定义在[﹣2,2]上的函数f(x)在区间[0,2]上单调递减,且f(1﹣m)<f(3m).
(1)若函数f(x)在区间[﹣2,2]上是奇函数,求实数m的取值范围;
(2)若函数f(x)在区间[﹣2,2]上是偶函数,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设m,p,q均为正数,且
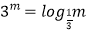 ,
,  ,
, 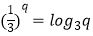 ,则( )
,则( )
A.m>p>q
B.p>m>q
C.m>q>p
D.p>q>m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( )
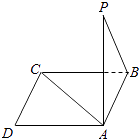
A.90°
B.60°
C.45°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,2,在Rt△ABC中,AB=BC=4,点E在线段AB上,过点E作交AC于点F,将△AEF沿EF折起到△PEF的位置(点A与P重合),使得∠PEB=60°.
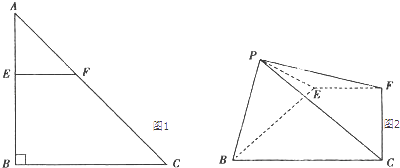
(1)求证:EF⊥PB;
(2)试问:当点E在何处时,四棱锥P﹣EFCB的侧面的面积最大?并求此时四棱锥P﹣EFCB的体积及直线PC与平面EFCB所成角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=-x3+ax,
(1)求a=3时,函数f(x)的单调区间;
(2)求a=12时,函数f(x)的极值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数g(x)=f(x)+2x,x∈R为奇函数.
(1)判断函数f(x)的奇偶性;
(2)若x>0时,f(x)=log3x,求函数g(x)的解析式.
相关试题

