
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)对该快递点近![]() 天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为
天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,那么从这
件,那么从这![]() 天中随机抽出
天中随机抽出![]() 天,求这
天,求这![]() 天的日揽包裹数均超过
天的日揽包裹数均超过![]() 件的概率.
件的概率.
【答案】(1)![]() 一个包裹,
一个包裹,![]() 一个包裹时花费的运费最少,为
一个包裹时花费的运费最少,为![]() 元;(2)
元;(2)![]() .
.
【解析】
(1)分![]() 一个包裹,
一个包裹,![]() 一个包裹,
一个包裹,![]() 一个包裹,
一个包裹,![]() 一个包裹,
一个包裹,![]() 一个包裹,
一个包裹,![]() 一个包裹三种情况讨论;
一个包裹三种情况讨论;
(2)采用枚举法,枚举出基本事件总数以及事件“![]() 天的日揽包裹数均超过
天的日揽包裹数均超过![]() 件”所包含的基本事件个数,再利用古典概型的概率计算公式计算即可.
件”所包含的基本事件个数,再利用古典概型的概率计算公式计算即可.
解:![]() 一个包裹,
一个包裹,![]() 一个包裹时,需花费
一个包裹时,需花费![]() (元),
(元),
![]() 一个包裹,
一个包裹,![]() 一个包裹时,需花费
一个包裹时,需花费![]() (元),
(元),
![]() 一个包裹,
一个包裹,![]() 一个包裹时,需花费
一个包裹时,需花费![]() (元),
(元),
综上,![]() 一个包裹,
一个包裹,![]() 一个包裹时花费的运费最少,为
一个包裹时花费的运费最少,为![]() 元.
元.
![]() 天中有
天中有![]() 天的日揽包裹数超过
天的日揽包裹数超过![]() 件,
件,
记这三天为![]() 其余两天为
其余两天为![]()
从![]() 天中随机抽出
天中随机抽出![]() 天的所有基本事件如下:
天的所有基本事件如下:
![]() ,
,![]() ,
,![]()
一共![]() 种,
种,
![]() 天的日揽包裹数均超过
天的日揽包裹数均超过![]() 件的基本事件有,
件的基本事件有,![]() 一共
一共![]() 种,
种,
所以从这![]() 天中随机抽出
天中随机抽出![]() 天,
天,
![]() 天的日揽件数均超过
天的日揽件数均超过![]() 件的概率为
件的概率为![]()


科目:高中数学 来源: 题型:
【题目】已知抛物线C:x24py(p为大于2的质数)的焦点为F,过点F且斜率为k(k0)的直线交C于A,B两点,线段AB的垂直平分线交y轴于点E,抛物线C在点A,B处的切线相交于点G.记四边形AEBG的面积为S.
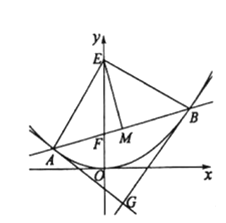
(1)求点G的轨迹方程;
(2)当点G的横坐标为整数时,S是否为整数?若是,请求出所有满足条件的S的值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】.极坐标系于直角坐标系![]() 有相同的长度单位,以原点
有相同的长度单位,以原点![]() 为极点,以
为极点,以![]() 正半轴为极轴.已知曲线
正半轴为极轴.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() ,
,![]() ,
,![]() ,
,![]() 与曲线
与曲线![]() 分别交异于极点
分别交异于极点![]() 的四点
的四点![]() .
.
(1)若曲线![]() 关于曲线
关于曲线![]() 对称,求
对称,求![]() 的值,并把曲线
的值,并把曲线![]() 和
和![]() 化成直角坐标方程;
化成直角坐标方程;
(2)设![]() ,当
,当![]() 时,求
时,求![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆台![]() 的轴截面为等腰梯形
的轴截面为等腰梯形![]() ,
,![]() 圆台
圆台![]() 的侧面积为
的侧面积为![]() .若点
.若点![]() 分别为圆
分别为圆![]() 上的动点,且点
上的动点,且点![]() 在平面
在平面![]() 的同侧.
的同侧.

(1)求证:![]() ;
;
(2)若![]() ,则当三棱锥
,则当三棱锥![]() 的体积取最大值时,求多面体
的体积取最大值时,求多面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)为了解该快递点2019年的揽件情况,在2019年内随机抽查了![]() 天的日揽收包裹数(单位:件),得到如下表格:
天的日揽收包裹数(单位:件),得到如下表格:
包裹数(单位:件) |
|
|
|
|
天数(天) |
|
|
|
|
现用这![]() 天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取
天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取![]() 天,记这
天,记这![]() 天中日揽收包裹数超过
天中日揽收包裹数超过![]() 件的天数为随机变量
件的天数为随机变量![]() 求
求![]() 的分布列和期望
的分布列和期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若数列![]() 满足所有的项均由
满足所有的项均由![]() 构成且其中
构成且其中![]() 有
有![]() 个,
个,![]() 有
有![]() 个
个![]() ,则称
,则称![]() 为“
为“![]() ﹣数列”.
﹣数列”.
(1)![]() 为“
为“![]() ﹣数列”
﹣数列”![]() 中的任意三项,则使得
中的任意三项,则使得![]() 的取法有多少种?
的取法有多少种?
(2)![]() 为“
为“![]() ﹣数列”
﹣数列”![]() 中的任意三项,则存在多少正整数
中的任意三项,则存在多少正整数![]() 对使得
对使得![]() 且
且![]() 的概率为
的概率为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
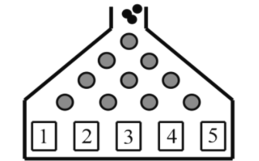
【题目】如图,高尔顿板是英国生物统计学家高尔顿设计的用来研究随机现象的模型,它是在一块竖起的木板上钉上一排排互相平行,水平间隔相等的圆柱形铁钉,并且每一排钉子数目都比上一排多一个,一排中各个钉子恰好对准上面一排两相邻铁钉的正中央,从入口处放入一个直径略小于两颗钉子间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两钉的间隙,又碰到下一排铁钉,如此继续下去,在最底层的5个出口处各放置一个容器接住小球,那么,小球落入1号容器的概率是______,若取4个小球进行试验,设其中落入4号容器的小球个数为x,则x的数学期望是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com