
【题目】定义:若数列![]() 满足所有的项均由
满足所有的项均由![]() 构成且其中
构成且其中![]() 有
有![]() 个,
个,![]() 有
有![]() 个
个![]() ,则称
,则称![]() 为“
为“![]() ﹣数列”.
﹣数列”.
(1)![]() 为“
为“![]() ﹣数列”
﹣数列”![]() 中的任意三项,则使得
中的任意三项,则使得![]() 的取法有多少种?
的取法有多少种?
(2)![]() 为“
为“![]() ﹣数列”
﹣数列”![]() 中的任意三项,则存在多少正整数
中的任意三项,则存在多少正整数![]() 对使得
对使得![]() 且
且![]() 的概率为
的概率为![]() .
.
【答案】(1)16;(2)115.
【解析】
(1)易得使得![]() 的情况只有“
的情况只有“![]() ”,“
”,“![]() ”两种,再根据组合的方法求解两种情况分别的情况数再求和即可.
”两种,再根据组合的方法求解两种情况分别的情况数再求和即可.
(2)易得“![]() ”共有
”共有![]() 种,“
种,“![]() ”共有
”共有![]() 种.再根据古典概型的方法可知
种.再根据古典概型的方法可知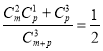 ,利用组合数的计算公式可得
,利用组合数的计算公式可得![]() ,当
,当![]() 时根据题意有
时根据题意有![]() ,共
,共![]() 个;
个;
当![]() 时求得
时求得![]() ,再根据
,再根据![]() 换元根据整除的方法求解满足的正整数对即可.
换元根据整除的方法求解满足的正整数对即可.
解:(1)三个数乘积为![]() 有两种情况:“
有两种情况:“![]() ”,“
”,“![]() ”,
”,
其中“![]() ”共有:
”共有:![]() 种,
种,
“![]() ”共有:
”共有:![]() 种,
种,
利用分类计数原理得:
![]() 为“
为“![]() ﹣数列”
﹣数列”![]() 中的任意三项,
中的任意三项,
则使得![]() 的取法有:
的取法有:![]() 种.
种.
(2)与(1)同理,“![]() ”共有
”共有![]() 种,
种,
“![]() ”共有
”共有![]() 种,
种,
而在“![]() ﹣数列”中任取三项共有
﹣数列”中任取三项共有![]() 种,
种,
根据古典概型有: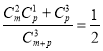 ,
,
再根据组合数的计算公式能得到:
![]() ,
,
![]() 时,应满足
时,应满足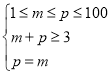 ,
,
![]() ,共
,共![]() 个,
个,
![]() 时,
时,
应满足 ,
,
视![]() 为常数,可解得
为常数,可解得![]() ,
,
![]()
![]() ,
,
根据![]() 可知,
可知,![]() ,
,
![]() ,
,
![]() ,
,
根据![]() 可知,
可知,![]() ,(否则
,(否则![]() ),
),
下设![]() ,
,
则由于![]() 为正整数知
为正整数知![]() 必为正整数,
必为正整数,
![]() ,
,
![]() ,
,
化简上式关系式可以知道:![]() ,
,
![]() 均为偶数,
均为偶数,
![]() 设
设![]() ,
,
则![]()
![]() ,
,
由于![]() 中必存在偶数,
中必存在偶数,
![]() 只需
只需![]() 中存在数为
中存在数为![]() 的倍数即可,
的倍数即可,
![]() ,
,
![]() .
.
检验:![]() 符合题意,
符合题意,
![]() 共有
共有![]() 个,
个,
综上所述:共有![]() 个数对
个数对![]() 符合题意.
符合题意.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,以
,以![]() 的短轴为直径的圆与直线
的短轴为直径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .已知
.已知![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,若
为顶角的等腰直角三角形,若![]() 在直线
在直线![]() 的右下方,求
的右下方,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国庆节假期期间,某商场为掌握假期期间顾客购买商品人次,统计了10月1日7:00﹣23:00这一时间段内顾客购买商品人次,统计发现这一时间段内顾客购买商品共5000人次顾客购买商品时刻的的频率分布直方图如下图所示,其中时间段7:0011:00,11:0015:00,15:00~19:00,19:00~23:00,依次记作[7,11),[11,15),[15,19),[19,23].
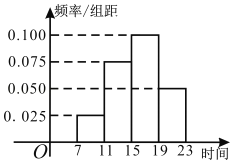
(1)求该天顾客购买商品时刻的中位数t与平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)由频率分布直方图可以近似认为国庆节假期期间该商场顾客购买商品时刻服从正态分布N(μ,δ2),其中μ近似为![]() ,δ=3.6,估计2019年国庆节假期期间(10月1日﹣10月7日)该商场顾客在12:12﹣19:24之间购买商品的总人次(结果保留整数);
,δ=3.6,估计2019年国庆节假期期间(10月1日﹣10月7日)该商场顾客在12:12﹣19:24之间购买商品的总人次(结果保留整数);
(3)为活跃节日气氛,该商场根据题中的4个时间段分组,采用分层抽样的方法从这5000个样本中随机抽取10个样本(假设这10个样本为10个不同顾客)作为幸运客户,再从这10个幸运客户中随机抽取4人每人奖励500元购物券,其他幸运客户每人奖励200元购物券,记获得500元购物券的4人中在15:00﹣19:00之间购买商品的人数为X,求X的分布列与数学期望;
参考数据:若T~N(μ,σ2),则①P(μ﹣σ<T≤μ+σ)=0.6827;②P(μ﹣2σ<T≤μ+2σ)=0.9545;③P(μ﹣3σ<T≤μ+3σ)=0.9973.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)对该快递点近![]() 天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为
天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,那么从这
件,那么从这![]() 天中随机抽出
天中随机抽出![]() 天,求这
天,求这![]() 天的日揽包裹数均超过
天的日揽包裹数均超过![]() 件的概率.
件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发商在其开发的某小区前修建了一个弓形景观湖.如图,该弓形所在的圆是以![]() 为直径的圆,且
为直径的圆,且![]() 米,景观湖边界
米,景观湖边界![]() 与
与![]() 平行且它们间的距离为
平行且它们间的距离为![]() 米.开发商计划从
米.开发商计划从![]() 点出发建一座景观桥(假定建成的景观桥的桥面与地面和水面均平行),桥面在湖面上的部分记作
点出发建一座景观桥(假定建成的景观桥的桥面与地面和水面均平行),桥面在湖面上的部分记作![]() .设
.设![]() .
.
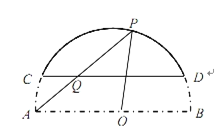
(1)用![]() 表示线段
表示线段![]() 并确定
并确定![]() 的范围;
的范围;
(2)为了使小区居民可以充分地欣赏湖景,所以要将![]() 的长度设计到最长,求
的长度设计到最长,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.

(1)求椭圆![]() 的方程;
的方程;
(2)如图,过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,连接
两点,连接![]() 并延长交
并延长交![]() 于
于![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com