
【题目】下列判断错误的是( )
A.若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
B.已知直线![]()
![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C.若随机变量![]() 服从二项分布:
服从二项分布: ![]() , 则
, 则![]()
D.![]() 是
是![]() 的充分不必要条件
的充分不必要条件
【答案】D
【解析】
根据正态分布、空间中点线面的位置关系、充分条件与必要条件的判断、二项分布及不等式的性质等知识,依次对四个选项加以分析判断,进而可求解.
对于![]() 选项,若随机变量
选项,若随机变量![]() 服从正态分布
服从正态分布![]() ,根据正态分布曲线的对称性,有
,根据正态分布曲线的对称性,有![]() ,故
,故![]() 选项正确,不符合题意;
选项正确,不符合题意;
对于![]() 选项,已知直线
选项,已知直线![]()
![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,则当
,则当![]() 时一定有
时一定有![]() ,充分性成立,而当
,充分性成立,而当![]() 时,不一定有
时,不一定有![]() ,故必要性不成立,所以“
,故必要性不成立,所以“![]() ”是“
”是“![]() ”的充分不必要条件,故
”的充分不必要条件,故![]() 选项正确,不符合题意;
选项正确,不符合题意;
对于![]() 选项,若随机变量
选项,若随机变量![]() 服从二项分布:
服从二项分布: ![]() , 则
, 则![]() ,故
,故![]() 选项正确,不符合题意;
选项正确,不符合题意;
对于![]() 选项,
选项,![]() ,仅当
,仅当![]() 时有
时有![]() ,当
,当![]() 时,
时,![]() 不成立,故充分性不成立;若
不成立,故充分性不成立;若![]() ,仅当
,仅当![]() 时有
时有![]() ,当
,当![]() 时,
时,![]() 不成立,故必要性不成立.
不成立,故必要性不成立.
因而![]() 是
是![]() 的既不充分也不必要条件,故
的既不充分也不必要条件,故![]() 选项不正确,符合题意.
选项不正确,符合题意.
故选:D


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系,将曲线![]() 上的每一个点的横坐标保持不变,纵坐标缩短为原来的
上的每一个点的横坐标保持不变,纵坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,
轴的正半轴为极轴,建立极坐标系, ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的参数方程;
的参数方程;
(Ⅱ)过原点![]() 且关于
且关于![]() 轴对称的两条直线
轴对称的两条直线![]() 与
与![]() 分别交曲线
分别交曲线![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() ,且点
,且点![]() 在第一象限,当四边形
在第一象限,当四边形![]() 的周长最大时,求直线
的周长最大时,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足bcosA﹣![]() asinB=0.
asinB=0.
(1)求A;
(2)已知a=2![]() ,B=
,B=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x24py(p为大于2的质数)的焦点为F,过点F且斜率为k(k0)的直线交C于A,B两点,线段AB的垂直平分线交y轴于点E,抛物线C在点A,B处的切线相交于点G.记四边形AEBG的面积为S.
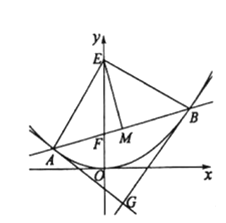
(1)求点G的轨迹方程;
(2)当点G的横坐标为整数时,S是否为整数?若是,请求出所有满足条件的S的值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为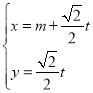 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(Ⅱ)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种电子产品,每件产品不合格的概率均为![]() ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验
,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验![]() 件该产品,且每 件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检 验方案:将产品每
件该产品,且每 件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检 验方案:将产品每![]() 个
个![]() 一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验
一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验![]() 次或
次或![]() 次.设该工厂生产
次.设该工厂生产![]() 件该产品,记每件产品的平均检验次 数为
件该产品,记每件产品的平均检验次 数为![]() .
.
(1)求![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)试说明,当![]() 越小时,该方案越合理,即所需平均检验次数越少;
越小时,该方案越合理,即所需平均检验次数越少;
(ii)当![]() 时,求使该方案最合理时
时,求使该方案最合理时![]() 的值及
的值及![]() 件该产品的平均检验次数.
件该产品的平均检验次数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电影《厉害了,我的国》于2018年3月正式登陆全国院线,网友纷纷表示,看完电影热血沸腾“我为我的国家骄傲,我为我是中国人骄傲!”《厉害了,我的国》正在召唤我们每一个人,不忘初心,用奋斗书写无悔人生,小明想约甲、乙、丙、丁四位好朋友一同去看《厉害了,我的国》,并把标识为![]() 的四张电影票放在编号分别为1,2,3,4的四个不同的盒子里,让四位好朋友进行猜测:
的四张电影票放在编号分别为1,2,3,4的四个不同的盒子里,让四位好朋友进行猜测:
甲说:第1个盒子里放的是![]() ,第3个盒子里放的是
,第3个盒子里放的是![]()
乙说:第2个盒子里放的是![]() ,第3个盒子里放的是
,第3个盒子里放的是![]()
丙说:第4个盒子里放的是![]() ,第2个盒子里放的是
,第2个盒子里放的是![]()
丁说:第4个盒子里放的是![]() ,第3个盒子里放的是
,第3个盒子里放的是![]()
小明说:“四位朋友你们都只说对了一半”
可以预测,第4个盒子里放的电影票为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)为了解该快递点2019年的揽件情况,在2019年内随机抽查了![]() 天的日揽收包裹数(单位:件),得到如下表格:
天的日揽收包裹数(单位:件),得到如下表格:
包裹数(单位:件) |
|
|
|
|
天数(天) |
|
|
|
|
现用这![]() 天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取
天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取![]() 天,记这
天,记这![]() 天中日揽收包裹数超过
天中日揽收包裹数超过![]() 件的天数为随机变量
件的天数为随机变量![]() 求
求![]() 的分布列和期望
的分布列和期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com