【题目】【2017江西师范大学附属中学三模】已知函数![]() 是自然对数的底数).
是自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,当
,当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(3)若![]() 且
且![]() ,求证:
,求证: ![]() .
.
参考答案:
【答案】(1)![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1) 求出![]() ,
, ![]() 得增区间,
得增区间, ![]() 得减区间;(2)利用导数研究函数
得减区间;(2)利用导数研究函数![]() 的单调性即可求函数
的单调性即可求函数![]() 的最大值;(3)化简已知得
的最大值;(3)化简已知得![]() ,
, ![]()
![]() 即
即![]() ,然后利用分析法证明原不等式.
,然后利用分析法证明原不等式.
试题解析: (1) ![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
令![]() ,
, ![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2) ![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() ,
,![]() ,
,![]()
当![]() 时,
时, ![]() ,
,![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
![]() .
.
(3) ![]() ,
, ![]()
![]() 即
即![]() .
.
由(1)知 ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,且
上单调递减,且![]() ,
,
则![]()
要证![]() ,即证
,即证![]() ,即证
,即证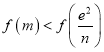 ,即证
,即证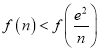 ,
,
即证![]() ,由于
,由于![]() ,即证
,即证![]() .
.
令![]()
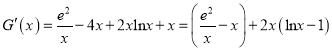
![]()
![]()
![]() 恒成立
恒成立
![]() 在
在![]() 递增,
递增, ![]() 在
在![]() 恒成立,
恒成立,
![]() 原不等式成立.
原不等式成立.
【方法点晴】本题主要考查的是利用导数研究函数的单调性、利用导数研究函数的最值、不等式的恒成立,属于难题.利用导数研究函数![]() 的单调性进一步求函数最值的步骤:①确定函数
的单调性进一步求函数最值的步骤:①确定函数![]() 的定义域;②对
的定义域;②对![]() 求导;③令
求导;③令![]() ,解不等式得
,解不等式得![]() 的范围就是递增区间;令
的范围就是递增区间;令![]() ,解不等式得
,解不等式得![]() 的范围就是递减区间;④根据单调性求函数
的范围就是递减区间;④根据单调性求函数![]() 的极值及最值(闭区间上还要注意比较端点处函数值的大小).
的极值及最值(闭区间上还要注意比较端点处函数值的大小).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+ax+b(a,b∈R),
(1)若函数f(x)在区间[﹣1,1]上不单调,求实数a的取值范围;
(2)记M(a,b)是|f(x)|在区间[﹣1,1]上的最大值,证明:当|a|≥2时,M(a,b)≥2. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017南阳一中四模】设
 ,
,  满足约束条件
满足约束条件 若目标函数
若目标函数 的最小值为
的最小值为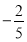 ,则实数
,则实数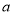 的值为
的值为A.
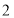 B.
B. 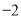 C.
C. 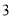 D.
D. 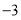
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个总体中含有4个个体,从中抽取一个容量为2的样本,说明为什么在抽取过程中每个个体被抽取的概率都相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=mx﹣1 , g(x)=﹣1+logmx(m>0,m≠1),有如下两个命题:
p:f(x)的定义域和g[f(x)]的值域相等.
q:g(x)的定义域和f[g(x)]的值域相等.
则( )
A.命题p,q都正确
B.命题p正确,命题q不正确
C.命题p,q都不正确
D.命题q不正确,命题p正确 -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017西安铁一中五模】已知函数
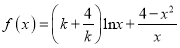 ,其中常数
,其中常数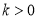 .
.(Ⅰ)讨论
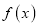 在
在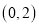 上的单调性;
上的单调性;(Ⅱ)当
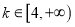 时,若曲线
时,若曲线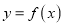 上总存在相异两点
上总存在相异两点 ,使曲线
,使曲线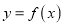 在
在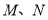 两点处的切线互相平行,试求
两点处的切线互相平行,试求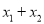 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2
 (a∈R),且f(1)>f(3),f(2)>f(3)( )
(a∈R),且f(1)>f(3),f(2)>f(3)( )
A.若k=1,则|a﹣1|<|a﹣2|
B.若k=1,则|a﹣1|>|a﹣2|
C.若k=2,则|a﹣1|<|a﹣2|
D.若k=2,则|a﹣1|>|a﹣2|
相关试题

