【题目】已知函数f(x)=2 ![]() (a∈R),且f(1)>f(3),f(2)>f(3)( )
(a∈R),且f(1)>f(3),f(2)>f(3)( )
A.若k=1,则|a﹣1|<|a﹣2|
B.若k=1,则|a﹣1|>|a﹣2|
C.若k=2,则|a﹣1|<|a﹣2|
D.若k=2,则|a﹣1|>|a﹣2|
参考答案:
【答案】D
【解析】解:分析各选项,只需讨论k=1和k=2两种情况,
①当k=1时,f(x)=2a﹣x , 在R上单调递减,
所以,必有f(1)>f(3),f(2)>f(3),
这两个式子对任意的实数a都成立,
因此,A选项和B选项都不能成立;
②当k=2时,f(x)= ![]() ,
,
f(x)在(﹣∞,a)单调递减,在(a,+∞)单调递增,
且函数f(x)的图象关于直线x=a轴对称,
又因为f(1)>f(3),f(2)>f(3),
结合函数图象可知,对称轴x=a> ![]() ,
,
因此,|a﹣1|>|a﹣2|.
所以答案是:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017江西师范大学附属中学三模】已知函数
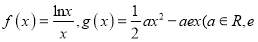 是自然对数的底数).
是自然对数的底数).(1)求函数
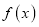 的单调区间;
的单调区间;(2)若
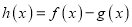 ,当
,当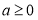 时,求函数
时,求函数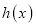 的最大值;
的最大值;(3)若
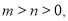 且
且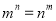 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=mx﹣1 , g(x)=﹣1+logmx(m>0,m≠1),有如下两个命题:
p:f(x)的定义域和g[f(x)]的值域相等.
q:g(x)的定义域和f[g(x)]的值域相等.
则( )
A.命题p,q都正确
B.命题p正确,命题q不正确
C.命题p,q都不正确
D.命题q不正确,命题p正确 -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017西安铁一中五模】已知函数
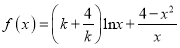 ,其中常数
,其中常数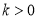 .
.(Ⅰ)讨论
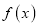 在
在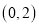 上的单调性;
上的单调性;(Ⅱ)当
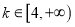 时,若曲线
时,若曲线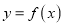 上总存在相异两点
上总存在相异两点 ,使曲线
,使曲线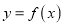 在
在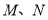 两点处的切线互相平行,试求
两点处的切线互相平行,试求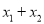 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有两个袋子,其中甲袋中装有编号分别为1、2、3、4的4个完全相同的球,乙袋中装有编号分别为2、4、6的3个完全相同的球.
(Ⅰ)从甲、乙袋子中各取一个球,求两球编号之和小于8的概率;
(Ⅱ)从甲袋中取2个球,从乙袋中取一个球,求所取出的3个球中含有编号为2的球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017衡阳第二次联考】已知函数
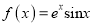 .
.(1)求函数
 的单调区间;
的单调区间;(2)如果对于任意的
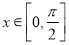 ,
,  恒成立,求实数
恒成立,求实数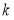 的取值范围;
的取值范围;(3)设函数
 ,
, 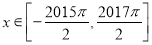 ,过点
,过点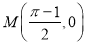 作函数
作函数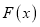 的图象的所有切线,令各切点的横坐标按从小到大构成数列
的图象的所有切线,令各切点的横坐标按从小到大构成数列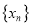 ,求数列
,求数列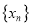 的所有项之和的值.
的所有项之和的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017省息一中第七次适应性考】已知函数
 (
(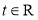 ),且
),且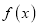 的导数为
的导数为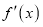 .
.(Ⅰ)若
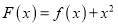 是定义域内的增函数,求实数
是定义域内的增函数,求实数 的取值范围;
的取值范围;(Ⅱ)若方程
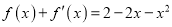 有3个不同的实数根,求实数
有3个不同的实数根,求实数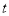 的取值范围.
的取值范围.
相关试题

