【题目】【2017南阳一中四模】设![]() ,
, ![]() 满足约束条件
满足约束条件 若目标函数
若目标函数![]() 的最小值为
的最小值为![]() ,则实数
,则实数![]() 的值为
的值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】
作出不等式组对应的平面区域图:(阴影部分![]() ).
).
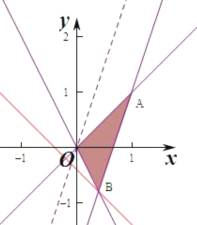
由![]() 得
得![]() ,平移直线
,平移直线![]() ,由图象可知当直线
,由图象可知当直线![]() 经过点
经过点![]() 时,直线
时,直线![]() 截距最小,此时
截距最小,此时![]() 最小,由
最小,由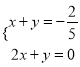 ,解得
,解得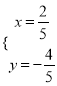 ,即
,即![]() ,同时
,同时![]() 也在直线
也在直线![]() 上 ,即
上 ,即![]() ,则
,则![]() ,故选A.
,故选A.
【方法点晴】本题主要考查可行域、含参数目标函数最优解和均值不等式求最值,属于难题.含参变量的线性规划问题是近年来高考命题的热点,由于参数的引入,提高了思维的技巧、增加了解题的难度, 此类问题的存在增加了探索问题的动态性和开放性,此类问题一般从目标函数的结论入手,对目标函数变化过程进行详细分析,对变化过程中的相关量的准确定位,是求最优解的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设偶函数f(x)的定义域为[﹣4,0)∪(0,4],若当x∈(0,4]时,f(x)=log2x,
(1)求出函数在定义域[﹣4,0)∪(0,4]的解析式;
(2)求不等式xf(x)<0得解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
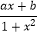 是定义在区间(﹣1,1)上的奇函数,且f(2)=
是定义在区间(﹣1,1)上的奇函数,且f(2)= 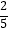 ,
,
(1)确定函数f(x)的解析式;
(2)用定义法证明f(x)在区间(﹣1,1)上是增函数;
(3)解不等式f(t﹣1)+f(t)<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+ax+b(a,b∈R),
(1)若函数f(x)在区间[﹣1,1]上不单调,求实数a的取值范围;
(2)记M(a,b)是|f(x)|在区间[﹣1,1]上的最大值,证明:当|a|≥2时,M(a,b)≥2. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个总体中含有4个个体,从中抽取一个容量为2的样本,说明为什么在抽取过程中每个个体被抽取的概率都相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017江西师范大学附属中学三模】已知函数
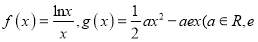 是自然对数的底数).
是自然对数的底数).(1)求函数
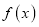 的单调区间;
的单调区间;(2)若
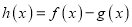 ,当
,当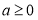 时,求函数
时,求函数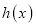 的最大值;
的最大值;(3)若
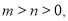 且
且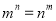 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=mx﹣1 , g(x)=﹣1+logmx(m>0,m≠1),有如下两个命题:
p:f(x)的定义域和g[f(x)]的值域相等.
q:g(x)的定义域和f[g(x)]的值域相等.
则( )
A.命题p,q都正确
B.命题p正确,命题q不正确
C.命题p,q都不正确
D.命题q不正确,命题p正确
相关试题

