【题目】已知命题p:若x>0,则函数y=x+ ![]() 的最小值为1,命题q:若x>1,则x2+2x﹣3>0,则下列命题是真命题的是( )
的最小值为1,命题q:若x>1,则x2+2x﹣3>0,则下列命题是真命题的是( )
A.p∨q
B.p∧q
C.(¬p)∧(¬q)
D.p∨(¬q)
参考答案:
【答案】A
【解析】解:x>0时,y=x+ ![]() ≥2
≥2 ![]() =
= ![]() ,
,
故命题p是假命题,
∵y=x2+2x﹣3=(x+1)2﹣4,对称轴x=﹣1,
函数在(1,+∞)递增,
∴x2+2x﹣3>0,
∴命题q是真命题,
∴p∨q是真命题,
故选:A.
【考点精析】通过灵活运用复合命题的真假,掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子装有六张卡片,上面分别写着如下六个函数:
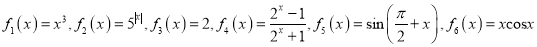 .
.(I)判断这
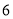 个函数的奇偶性;
个函数的奇偶性;(II)从中任意拿取两张卡片,若其中至少有一张卡片上写着的函数为奇函数.在此条件下,求两张卡片上写着的函数相加得到的新函数为奇函数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
 中,
中,  与
与 相交于点
相交于点 ,
,  平面
平面 ,
,  .
.
(I)求证:
 平面
平面 ;
;(II)当直线
 与平面
与平面 所成的角的余弦值为
所成的角的余弦值为 时,求证:
时,求证:  ;
;(III)在(II)的条件下,求异面直线
 与
与 所成的余弦值.
所成的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=3ax2+2bx+c,且有a+b+c=0,f(0)>0,f(1)>0.
(Ⅰ)求证:a>0,且﹣2<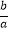 <﹣1;
<﹣1;
(Ⅱ)求证:函数y=f(x)在区间(0,1)内有两个不同的零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.57.2,3.6
B.57.2,56.4
C.62.8,63.6
D.62.8,3.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
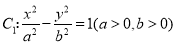 ,抛物线
,抛物线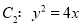 ,
, 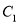 与
与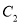 有公共的焦点
有公共的焦点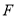 ,
, 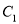 与
与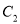 在第一象限的公共点为
在第一象限的公共点为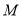 ,直线
,直线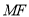 的倾斜角为
的倾斜角为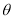 ,且
,且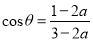 ,则关于双曲线的离心率的说法正确的是()
,则关于双曲线的离心率的说法正确的是()A. 仅有两个不同的离心率
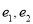 且
且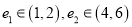 B. 仅有两个不同的离心率
B. 仅有两个不同的离心率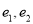 且
且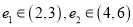 C. 仅有一个离心率
C. 仅有一个离心率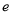 且
且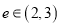 D. 仅有一个离心率
D. 仅有一个离心率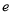 且
且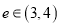
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
组号
分组
回答正确的人数
回答正确的人数占本组的比例
第1组
[18,28)
5
0.5
第2组
[28,38)
18
a
第3组
[38,48)
27
0.9
第4组
[48,58)
x
0.36
第5组
[58,68)
3
0.2
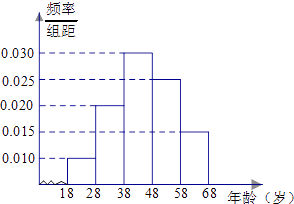
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
相关试题

