【题目】如图,在菱形![]() 中,
中, ![]() 与
与![]() 相交于点
相交于点![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.

(I)求证: ![]() 平面
平面![]() ;
;
(II)当直线![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() 时,求证:
时,求证: ![]() ;
;
(III)在(II)的条件下,求异面直线![]() 与
与![]() 所成的余弦值.
所成的余弦值.
参考答案:
【答案】(I)见解析;(II)见解析;(III)![]() .
.
【解析】试题分析:
(I)要证![]() 与平面
与平面![]() 垂直,只要证
垂直,只要证![]() 与平面
与平面![]() 内两条相交直线垂直即可,这由已知线面垂直可得一个,又由菱形对角线垂直又得一个,由此可证;(II)由已知线面垂直得
内两条相交直线垂直即可,这由已知线面垂直可得一个,又由菱形对角线垂直又得一个,由此可证;(II)由已知线面垂直得![]() 平面
平面![]() ,从而知
,从而知![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,从而可得
所成的角,从而可得![]() ,然后计算出三线段
,然后计算出三线段![]() 的长,由勾股定理逆定理可得垂直;
的长,由勾股定理逆定理可得垂直;
(III)取![]() 中点
中点![]() ,则有
,则有![]() ,从而可得异面直线所成的角,再解相应三角形可得.
,从而可得异面直线所成的角,再解相应三角形可得.
试题解析:
(I)![]() 平面
平面![]()
![]() ;
;
(II)![]() 平面
平面![]() 直线
直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 而且
而且![]() 中,
中, ![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() 中
中![]() 中
中![]() 中
中![]() ;
;
(III)取![]() 边的中点
边的中点![]() ,连接
,连接![]() 且
且![]() 为所求的角或其补角,而在
为所求的角或其补角,而在![]() 中,
中, ![]() 中
中![]()
![]() 异面直线
异面直线![]() 与
与![]() 所成的余弦值为
所成的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知D是以点A(4,1),B(﹣1,﹣6),C(﹣2,3)为顶点的三角形区域(包括边界及内部).
(1)写出表示区域D的不等式组;
(2)设点B(﹣1,﹣6)、C(﹣2,3)在直线4x﹣3y﹣a=0的异侧,求a的取值范围;
(3)若目标函数z=kx+y(k<0)的最小值为﹣k﹣6,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x>0,y>0,且2x+8y﹣xy=0,求:
(1)xy的最小值;
(2)x+y的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子装有六张卡片,上面分别写着如下六个函数:
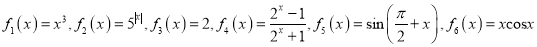 .
.(I)判断这
 个函数的奇偶性;
个函数的奇偶性;(II)从中任意拿取两张卡片,若其中至少有一张卡片上写着的函数为奇函数.在此条件下,求两张卡片上写着的函数相加得到的新函数为奇函数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=3ax2+2bx+c,且有a+b+c=0,f(0)>0,f(1)>0.
(Ⅰ)求证:a>0,且﹣2<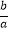 <﹣1;
<﹣1;
(Ⅱ)求证:函数y=f(x)在区间(0,1)内有两个不同的零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:若x>0,则函数y=x+
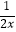 的最小值为1,命题q:若x>1,则x2+2x﹣3>0,则下列命题是真命题的是( )
的最小值为1,命题q:若x>1,则x2+2x﹣3>0,则下列命题是真命题的是( )
A.p∨q
B.p∧q
C.(¬p)∧(¬q)
D.p∨(¬q) -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.57.2,3.6
B.57.2,56.4
C.62.8,63.6
D.62.8,3.6
相关试题

