【题目】已知数列{an}的前n项和为Sn , 且Sn=2an﹣2(n∈N*),数列{bn}满足b1=1,且点P(bn , bn+1)(n∈N*)在直线y=x+2上.
(1)求数列{an}、{bn}的通项公式;
(2)求数列{anbn}的前n项和Dn;
(3)设cn=ansin2 ![]() ,求数列{cn}的前2n项和T2n .
,求数列{cn}的前2n项和T2n .
参考答案:
【答案】
(1)解:当n=1,a1=2
当n≥2时,an=Sn﹣Sn﹣1=2an﹣2an﹣1
∴an=2an﹣1(n≥2),∴{an}是等比数列,公比为2,首项a1=2
∴ ![]()
又点 ![]() 在直线y=x+2上,∴bn+1=bn+2,
在直线y=x+2上,∴bn+1=bn+2,
∴{bn}是等差数列,公差为2,首项b1=1,∴bn=2n﹣1
(2)解:∵ ![]()
∴ ![]() ①
①
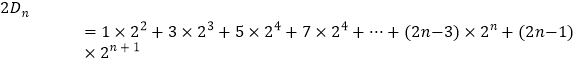 ②
②
①﹣②得 ![]()
= ![]()
![]()
(3)解: ![]()
T2n=(a1+a3+…+a2n﹣1)﹣(b2+b4+…b2n)
= ![]()
【解析】(1)利用数列递推式,再写一式,两式相减,可求求数列{an}的通项公式;利用点 ![]() 在直线y=x+2上,可得{bn}是等差数列,公差为2,首项b1=1,从而可求{bn}的通项公式;(2)利用错位相减法,可求数列{anbn}的前n项和Dn;(3)利用分组求和法,可求数列{cn}的前2n项和T2n .
在直线y=x+2上,可得{bn}是等差数列,公差为2,首项b1=1,从而可求{bn}的通项公式;(2)利用错位相减法,可求数列{anbn}的前n项和Dn;(3)利用分组求和法,可求数列{cn}的前2n项和T2n .
【考点精析】掌握数列的前n项和是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,左顶点为A,左焦点为F1(﹣2,0),点B(2,
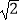 )在椭圆C上,直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
)在椭圆C上,直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
(Ⅰ)求椭圆C的方程;
(Ⅱ)在x轴上是否存在点P,使得无论非零实数k怎样变化,总有∠MPN为直角?若存在,求出点P的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,分别测出它们的高度如下(单位:cm)
甲:19 20 21 23 25 29 32 33 37 41
乙:10 24 26 30 34 37 44 46 47 48
(1)用茎叶图表示上述两组数据,并对两块地抽取树苗的高度进行比较,写出一个统计结论;
(2)苗圃基地分配这20株树苗的栽种任务,小王在苗高大于40cm的5株树苗中随机的选种2株,则小王没有选到甲苗圃树苗的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=2px(p>0)的焦点为F,若过点F且斜率为1的直线与抛物线相交于M,N两点,且|MN|=8.
(1)求抛物线C的方程;
(2)设直线l为抛物线C的切线,且l∥MN,P为l上一点,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b是异面直线,直线c∥a,则c与b的位置关系是( )
A.异面或相交
B.相交
C.异面
D.平行 -
科目: 来源: 题型:
查看答案和解析>>【题目】 【2017四川宜宾二诊】选修4-4:坐标系与参数方程
在直角坐标系
 中,已知点
中,已知点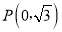 ,曲线
,曲线 的参数方程为
的参数方程为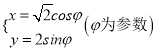 .以原点为极点,
.以原点为极点, 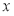 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为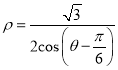 .
. (Ⅰ)判断点
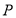 与直线
与直线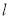 的位置关系并说明理由;
的位置关系并说明理由; (Ⅱ)设直线
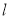 与曲线
与曲线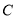 的两个交点分别为
的两个交点分别为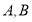 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017江西南昌十所重点二模】选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为
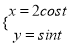 (t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:
(t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2: 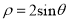 .
.(Ⅰ)求曲线C1和C2的直角坐标方程,并分别指出其曲线类型;
(Ⅱ)试判断:曲线C1和C2是否有公共点?如果有,说明公共点的个数;如果没有,请说明理由;
(Ⅲ)设
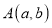 是曲线C1上任意一点,请直接写出a + 2b的取值范围.
是曲线C1上任意一点,请直接写出a + 2b的取值范围.
相关试题

