【题目】已知函数f(x)=bax , (其中a,b为常数且a>0,a≠1)的图象经过点A(1,8),B(3,32)
(1)求f(x)的解析式;
(2)若不等式![]() +1﹣2m≥0在x∈(﹣∞,1]上恒成立,求实数m的取值范围.
+1﹣2m≥0在x∈(﹣∞,1]上恒成立,求实数m的取值范围.
参考答案:
【答案】解:(1)把点A(1,8),B(3,32)代入函数f(x)=bax , 可得![]() ,求得
,求得![]() ,∴f(x)=42x .
,∴f(x)=42x .
(2)不等式![]() +1﹣2m≥0,即 m≤
+1﹣2m≥0,即 m≤![]() [
[![]() ]2+
]2+![]()
![]() +
+![]() .
.
令t=![]() ,则 m≤
,则 m≤![]() t2+
t2+![]() t+
t+![]() .
.
记g(t)=![]() t2+
t2+![]() t+
t+![]() =
=![]() (t+
(t+![]() )2+
)2+![]() ,由x∈(﹣∞,1],可得t≥
,由x∈(﹣∞,1],可得t≥![]() .
.
故当t=![]() 时,函数g(t)取得最小值为
时,函数g(t)取得最小值为![]() .
.
由题意可得,m≤g(t)min , ∴m≤![]() .
.
【解析】(1)把点A(1,8),B(3,32)代入函数f(x)=bax , 求得a、b的值,可得f(x)的解析式.
(2)不等式即 m≤![]() [
[![]() ]2+
]2+![]()
![]() +
+![]() , 令t=
, 令t=![]() , 则 m≤
, 则 m≤![]() t2+
t2+![]() t+
t+![]() . 利用二次函数的性质求得g(t)=
. 利用二次函数的性质求得g(t)=![]() t2+
t2+![]() t+
t+![]() 的最小值,可得m的范围.
的最小值,可得m的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用二分法研究函数f(x)=x3+3x﹣1的零点时,第一次经计算f(0)<0,f(0.5)>0,可得其中一个零点x0∈ ,第二次应计算的f(x)的值为f( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ln(3+x)+ln(3﹣x).
(Ⅰ)求函数y=f(x)的定义域;
(Ⅱ)判断函数y=f(x)的奇偶性;
(Ⅲ)若f(2m﹣1)<f(m),求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 为等比数列,
为等比数列,  ,公比
,公比 ,且
,且 成等差数列.
成等差数列.(1)求数列
 的通项公式;
的通项公式;(2)设
 ,
,  ,求使
,求使 的
的 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正四棱柱
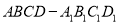 中,
中, 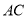 为底面
为底面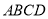 的对角线,
的对角线, 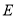 为
为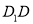 的中点.
的中点.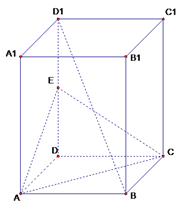
(1)求证:
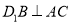 ;
;(2)求证:
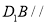 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
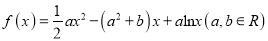
(Ⅰ)当
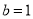 时,求函数
时,求函数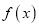 的单调区间;
的单调区间; (Ⅱ)当
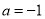 ,
,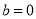 时,证明:
时,证明: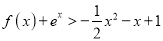 (其中
(其中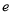 为自然对数的底数).
为自然对数的底数). -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|1﹣
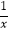 |
|
(1)求满足f(x)=2的x值;
(2)是否存在实数a,b,且0<a<b<1,使得函数y=f(x)在区间[a,b]上的值域为[a,2b],若存在,求出a,b的值;若不存在,请说明理由.
相关试题

