【题目】(本题满分12分)某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,用最小二乘法求出y与x的回归方程![]() ;
;
(3)预测销售额为115万元时,大约需要多少万元广告费。
参考公式:回归方程为![]() 其中
其中 ,
, ![]()
参考答案:
【答案】(1)具有相关关系;(2)![]() ;(3)15
;(3)15
【解析】试题分析:(Ⅰ)根据表格中所给的数据,写出对应的点的坐标,在直角坐标系中描出这几个点,得到散点图;(Ⅱ)首先做出这组数据的横标和纵标的平均数,利用最小二乘法做出线性回归方程的系数,根据样本中心点在线性回归直线上,求出a的值,写出线性回归方程;(Ⅲ)根据上一问做出的线性回归方程,当y的值是一个确定的值时,把值代入做出对应的x的值
试题解析:(1)散点图如图

由图可判断:广告费与销售额具有相关关系。
(2)![]() ,
,![]()
![]() =
=![]() =
=![]()
![]() =
=![]() =
=![]()
 =
=![]() =
=![]()
![]() =
=![]() =
=![]()
∴线性回归方程为![]()
(3)由题得:![]() ,
,![]() ,得
,得![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·桂林高二检测)如图所示,在四边形ABCD中,AB=AD=CD=1,BD=
 ,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是________.
,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是________.
(1)A′C⊥BD.(2)∠BA′C=90°.
(3)CA′与平面A′BD所成的角为30°.
(4)四面体A′-BCD的体积为
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称为“局部奇函数”
,则称为“局部奇函数”(1)已知二次函数
 (
( 且
且 ),试判断
),试判断 是否为“局部奇函数”,并说明理由;
是否为“局部奇函数”,并说明理由;(2)若
 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;(3)若
 为定义域为
为定义域为 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知随机变量
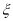 的取值为不大于
的取值为不大于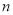 的非负整数值,它的分布列为:
的非负整数值,它的分布列为:
0
1
2
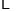
n
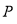
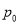
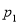
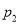
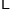
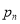
其中
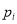 (
(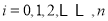 )满足:
)满足: 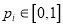 ,且
,且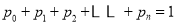 .
.定义由
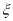 生成的函数
生成的函数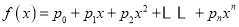 ,令
,令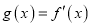 .
.(I)若由
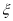 生成的函数
生成的函数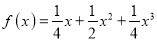 ,求
,求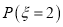 的值;
的值;(II)求证:随机变量
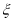 的数学期望
的数学期望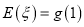 ,
, 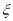 的方差
的方差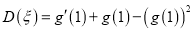 ;
;(
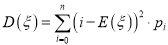 )
)(Ⅲ)现投掷一枚骰子两次,随机变量
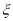 表示两次掷出的点数之和,此时由
表示两次掷出的点数之和,此时由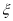 生成的函数记为
生成的函数记为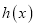 ,求
,求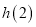 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
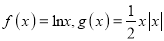
.
(1)求

在
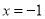
处的切线方程;
(2)令

,求

的单调区间;
(3)若任意

且

,都有
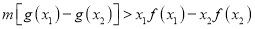
恒成立,求实数
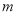
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,定义域为
 上的函数
上的函数 是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.
是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.
(1)求
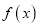 的解析式;
的解析式;(2)若
 关于的方程
关于的方程 有三个不同解,求
有三个不同解,求 的取值范围;
的取值范围;(3)若
 ,求
,求 的取值集合.
的取值集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)分析,你认为选派哪位学生参加合适?请说明理由
参考公式:

相关试题

