【题目】等比数列{an}中,a2﹣a1=2,且2a2为3a1和a3的等差中项.
(1)求数列{an}的通项公式;
(2)设bn=2log3an+1,且数列{ ![]() }的前n项和为Tn . 求Tn .
}的前n项和为Tn . 求Tn .
参考答案:
【答案】
(1)解:设等比数列{an}的公比为q,∵2a2为3a1和a3的等差中项,∴2×2a2=3a1+a3,化为4a1q= ![]() ,∴q2﹣4q+3=0,
,∴q2﹣4q+3=0,
解得q=1或3.又a2﹣a1=2,∴a1(q﹣1)=2,q≠1,∴ ![]() .
.
∴an=3n﹣1
(2)解:bn=2log3an+1=2n﹣1,
∴ ![]() =
= ![]() =
= ![]() .
.
∴数列{ ![]() }的前n项和为Tn=
}的前n项和为Tn= ![]()
= ![]()
= ![]() .
.
【解析】(1)设等比数列{an}的公比为q,由2a2为3a1和a3的等差中项,可得2×2a2=3a1+a3 , 利用等比数列的通项公式代入化简为q2﹣4q+3=0, 解得q.又a2﹣a1=2,a1(q﹣1)=2,q≠1,解出即可得出.(2)bn=2log3an+1=2n﹣1,可得 ![]() =
= ![]() =
= ![]() .再利用“裂项求和”方法即可得出.
.再利用“裂项求和”方法即可得出.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系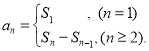 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第
 年与年销量
年与年销量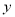 (单位:万件)之间的关系如下表:
(单位:万件)之间的关系如下表:
(1)在图中画出表中数据的散点图;
(2)根据散点图选择合适的回归模型拟合
 与
与 的关系(不必说明理由);
的关系(不必说明理由);(3)建立
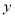 关于
关于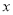 的回归方程,预测第5年的销售量.
的回归方程,预测第5年的销售量.附注:参考公式:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
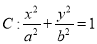 (
(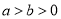 ),若椭圆
),若椭圆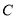 上的一动点到右焦点的最短距离为
上的一动点到右焦点的最短距离为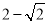 ,且右焦点到直线
,且右焦点到直线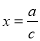 的距离等于短半轴的长,已知
的距离等于短半轴的长,已知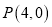 ,过
,过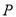 的直线与椭圆交于
的直线与椭圆交于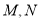 两点.
两点.(1)求椭圆
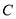 的方程;
的方程;(2)求
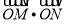 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
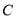 的中心在原点,焦点在
的中心在原点,焦点在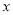 轴上,离心率
轴上,离心率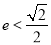 .以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为
.以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为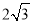 .
.(Ⅰ)求椭圆
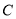 的方程;
的方程;(Ⅱ)若点
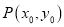 为椭圆
为椭圆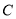 上一点,直线
上一点,直线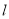 的方程为
的方程为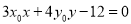 ,求证:直线
,求证:直线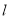 与椭圆
与椭圆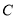 有且只有一个交点.
有且只有一个交点. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知cosA=
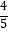 ,b=5c.
,b=5c.
(1)求sinC;
(2)若△ABC的面积S= sinBsinC,求a的值.
sinBsinC,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是2017年第一季度五省
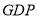 情况图,则下列陈述正确的是( )
情况图,则下列陈述正确的是( )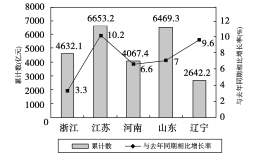
①2017年第一季度
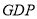 总量和增速均居同一位的省只有1个;
总量和增速均居同一位的省只有1个;②与去年同期相比,2017年第一季度五个省的
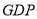 总量均实现了增长;
总量均实现了增长;③去年同期的
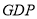 总量前三位是江苏、山东、浙江;
总量前三位是江苏、山东、浙江;④2016年同期浙江的
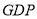 总量也是第三位.
总量也是第三位.A. ①② B. ②③④ C. ②④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
,  (
( ).
).(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)若函数
 在
在 处取得极大值,求正实数
处取得极大值,求正实数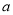 的取值范围.
的取值范围.
相关试题

