【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析: ![]() 表示一辆车从甲地到乙地遇到红灯的个数,
表示一辆车从甲地到乙地遇到红灯的个数, ![]() 的所有可能取值为0,1,2,3.分别求出相应的概率值,列出随机变量
的所有可能取值为0,1,2,3.分别求出相应的概率值,列出随机变量![]() 的分布列并计算数学期望,
的分布列并计算数学期望, ![]() 表示第一辆车遇到红灯的个数,
表示第一辆车遇到红灯的个数, ![]() 表示第二辆车遇到红灯的个数,这2辆车共遇到1个红灯就是包括第一辆遇到1次红灯且第2辆没遇上和第一辆没遇上红灯且第2辆遇上1次红灯两个事件的概率的和.
表示第二辆车遇到红灯的个数,这2辆车共遇到1个红灯就是包括第一辆遇到1次红灯且第2辆没遇上和第一辆没遇上红灯且第2辆遇上1次红灯两个事件的概率的和.
试题解析:(Ⅰ)解:随机变量![]() 的所有可能取值为0,1,2,3.
的所有可能取值为0,1,2,3.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以,随机变量![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
随机变量![]() 的数学期望
的数学期望![]() .
.
(Ⅱ)解:设![]() 表示第一辆车遇到红灯的个数,
表示第一辆车遇到红灯的个数, ![]() 表示第二辆车遇到红灯的个数,则所求事件的概率为
表示第二辆车遇到红灯的个数,则所求事件的概率为![]()
![]() .
.
所以,这2辆车共遇到1个红灯的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某零售店近5个月的销售额和利润额资料如下表:
商店名称





销售额
 /千万元
/千万元3
5
6
7
9
利润额
 /百万元
/百万元2
3
3
4
5
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额
 关于销售额
关于销售额 的回归直线方程;
的回归直线方程;(3)当销售额为4千万元时,利用(2)的结论估计该零售店的利润额(百万元).
[参考公式:
 ,
, ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,点
中,点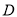 是
是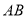 的中点.
的中点.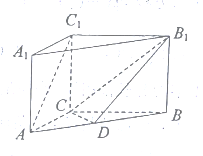
(1)求证:
 平面
平面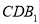 ;
;(2)若
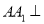 平面
平面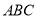 ,
, 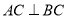 ,
, 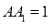 ,
, 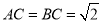 ,求二面角
,求二面角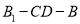 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
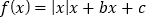 ,则下列命题中正确的个数是( )
,则下列命题中正确的个数是( )①当
 时,函数
时,函数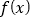 在
在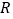 上是单调增函数;
上是单调增函数;②当
 时,函数
时,函数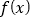 在
在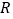 上有最小值;
上有最小值;③函数
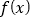 的图象关于点
的图象关于点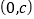 对称;
对称;④方程
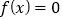 可能有三个实数根.
可能有三个实数根.A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过随机询问72名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
男
女
总计
读营养说明
16
28
44
不读营养说明
20
8
28
总计
36
36
72
(1)根据以上列联表判断,能否在犯错误的概率不超过0.005的前提下认为性别和是否看营养说明有关系呢?
(2)从被询问的28名不读营养说明的大学生中,随机抽取2名学生,求抽到女生人数
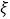
的分布列及数学期望.
附:
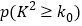
0.010
0.005
0.001
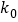
6.635
7.879
10.828
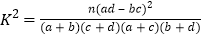
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=
 (|x﹣a2|+|x﹣2a2|﹣3a2),若x∈R,f(x﹣1)≤f(x),则实数a的取值范围为( )
(|x﹣a2|+|x﹣2a2|﹣3a2),若x∈R,f(x﹣1)≤f(x),则实数a的取值范围为( )
A.[﹣ ,
,  ]
]
B.[﹣ ,
,  ]
]
C.[﹣ ,
,  ]
]
D.[﹣ ,
,  ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系
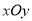 的原点,极轴为
的原点,极轴为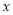 轴的正半轴,两种坐标系中的长度单位相同,已知曲线
轴的正半轴,两种坐标系中的长度单位相同,已知曲线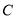 的极坐标方程为
的极坐标方程为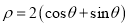 .
.(1)求
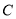 的直角坐标方程;
的直角坐标方程;(2)直线
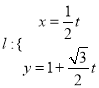 (
(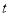 为参数)与曲线
为参数)与曲线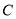 交于
交于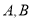 两点,与
两点,与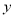 轴交于
轴交于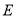 ,求
,求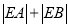 .
.
相关试题

